Which of the following pairs are identical?
f(x)=√x2,g(x)=(√x)2
f(x)=1√x2,g(x)=xx2
f(x)=log(x−1)+log(x−2),g(x)=log(x−1)(x−2)
None of these
The correct Answer is:D
To determine which of the given pairs of functions are identical, we will analyze each pair step by step.
Step 1: Analyze the first pair of functions
Let’s denote the first pair as:
- f(x)=√x2
- g(x)=√x2
Domain of f(x):
The function f(x)=√x2 is defined for all real numbers x. This is because the square root of a square is always non-negative. Thus, the domain of f(x) is:
Domain of f(x)=(−∞,∞)
Domain of g(x):
Similarly, g(x)=√x2 is also defined for all real numbers x. Therefore, the domain of g(x) is:
Domain of g(x)=(−∞,∞)
Conclusion for the first pair:
Since both functions have the same domain, they are identical.
Step 2: Analyze the second pair of functions
Let’s denote the second pair as:
- f(x)=1x
- g(x)=1x
Domain of f(x):
The function f(x)=1x is defined for all real numbers except x=0. Thus, the domain of f(x) is:
Domain of f(x)=(−∞,0)∪(0,∞)
Domain of g(x):
Similarly, g(x)=1x has the same domain:
Domain of g(x)=(−∞,0)∪(0,∞)
Conclusion for the second pair:
Since both functions have the same domain, they are identical.
Step 3: Analyze the third pair of functions
Let’s denote the third pair as:
- f(x)=log(x−1)+log(x−2)
- g(x)=log((x−1)(x−2))
Domain of f(x):
The function f(x) is defined when both x−1>0 and x−2>0. This means:
- x>1
- x>2
Thus, the domain of f(x) is:
Domain of f(x)=(2,∞)
Domain of g(x):
The function g(x) is defined when (x−1)(x−2)>0. This occurs when:
- x<1 or x>2
Thus, the domain of g(x) is:
Domain of g(x)=(−∞,1)∪(2,∞)
Conclusion for the third pair:
Since the domains of f(x) and g(x) are different, they are not identical.
Final Conclusion
The identical pairs are:
- Pair 1: f(x)=√x2 and g(x)=√x2
- Pair 2: f(x)=1x and g(x)=1x
Let’s denote the first pair as:
- f(x)=√x2
- g(x)=√x2
The function f(x)=√x2 is defined for all real numbers x. This is because the square root of a square is always non-negative. Thus, the domain of f(x) is:
Domain of f(x)=(−∞,∞)
Similarly, g(x)=√x2 is also defined for all real numbers x. Therefore, the domain of g(x) is:
Domain of g(x)=(−∞,∞)
Since both functions have the same domain, they are identical.
Let’s denote the second pair as:
- f(x)=1x
- g(x)=1x
The function f(x)=1x is defined for all real numbers except x=0. Thus, the domain of f(x) is:
Domain of f(x)=(−∞,0)∪(0,∞)
Similarly, g(x)=1x has the same domain:
Domain of g(x)=(−∞,0)∪(0,∞)
Since both functions have the same domain, they are identical.
Let’s denote the third pair as:
- f(x)=log(x−1)+log(x−2)
- g(x)=log((x−1)(x−2))
The function f(x) is defined when both x−1>0 and x−2>0. This means:
- x>1
- x>2
Domain of f(x)=(2,∞)
The function g(x) is defined when (x−1)(x−2)>0. This occurs when:
- x<1 or x>2
Domain of g(x)=(−∞,1)∪(2,∞)
Since the domains of f(x) and g(x) are different, they are not identical.
The identical pairs are:
- Pair 1: f(x)=√x2 and g(x)=√x2
- Pair 2: f(x)=1x and g(x)=1x
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Test Yourself15videos
FUNCTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Practice Exercises (Standard Level)30videos
FUNCTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - TEST YOURSELF15videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - FundamentalsEXERCISE - Test Yourself15videos
Fundamentals
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following pairs have identical bond order?
AF2andO2−2BN2andCO2CO2andO−2DN2andN+2 - Question 2 - Select One
Which of the following pairs have identical values of e/m?
AA proton and a neutronBA proton and deuterium,CDeiterium and α-particleDAn electron and γ-rays - Question 3 - Select One
Which of the following pairs have identical values of e/m?
AA proton and a neutronBA proton and deuteriumCDeuterium and an alpha- particleDAn electron and gama rays
Which of the following pairs has identical shape?
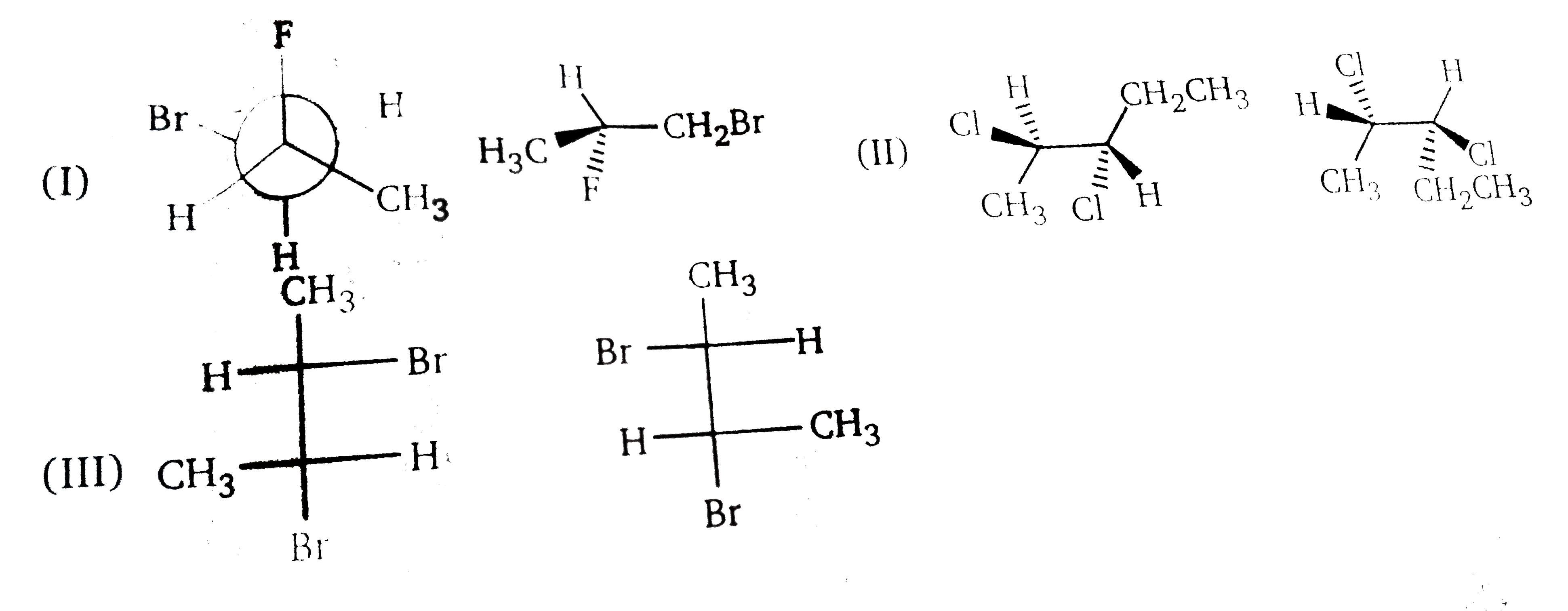
View SolutionIndicate whether each of the following pairs are identical, or?
 View Solution
View SolutionWhich of the following has //have identical nond order ?
View SolutionWhich of the following pairs have identical bond order?
View SolutionWhich of the following is an identity ?
View Solution