If the ratio of boys to girls in a class is B and the ratio of girls to boys is G, then 3 (B + G) is :
equal to 3
less than 3
more than 3
less than 13
The correct Answer is:C
To solve the problem, we need to express the ratios of boys to girls and girls to boys mathematically, and then calculate the value of 3(B+G).
1. Define the Variables:
Let the number of boys be X and the number of girls be Y.
2. Express the Ratios:
- The ratio of boys to girls is given as B=XY.
- The ratio of girls to boys is given as G=YX.
3. Calculate B+G:
- We can express B+G as:
B+G=XY+YX
- To combine these fractions, we need a common denominator:
B+G=X2+Y2XY
4. Calculate 3(B+G):
- Now, we can find 3(B+G):
3(B+G)=3(X2+Y2XY)=3(X2+Y2)XY
5. Analyze the Expression:
- Since X and Y are positive integers, we can analyze the term X2+Y2XY.
- By the Cauchy-Schwarz inequality, we know that:
(X+Y)2≤2(X2+Y2)
- This implies that:
X2+Y2XY≥1
- Therefore, 3(B+G)=3(X2+Y2)XY>3.
Final Result:
Thus, we conclude that 3(B+G)>3.
Let the number of boys be X and the number of girls be Y.
- The ratio of boys to girls is given as B=XY.
- The ratio of girls to boys is given as G=YX.
- We can express B+G as:
B+G=XY+YX
- To combine these fractions, we need a common denominator:
B+G=X2+Y2XY
- Now, we can find 3(B+G):
3(B+G)=3(X2+Y2XY)=3(X2+Y2)XY
- Since X and Y are positive integers, we can analyze the term X2+Y2XY.
- By the Cauchy-Schwarz inequality, we know that:
(X+Y)2≤2(X2+Y2)
- This implies that:
X2+Y2XY≥1
- Therefore, 3(B+G)=3(X2+Y2)XY>3.
Thus, we conclude that 3(B+G)>3.
Topper's Solved these Questions
- RATIO,PROPORTION AND VARIATIONBook:DISHA PUBLICATIONChapter:RATIO,PROPORTION AND VARIATIONExercise:Test Yourself
Explore 15 Videos
- RATIO,PROPORTION AND VARIATIONBook:DISHA PUBLICATIONChapter:RATIO,PROPORTION AND VARIATIONExercise:Practice Exercises ( Standard Level)
Explore 26 Videos
- QUADRATIC AND CUBIC EQUATIONSBook:DISHA PUBLICATIONChapter:QUADRATIC AND CUBIC EQUATIONSExercise:Test Yourself
Explore 15 Videos
- SET THEORYBook:DISHA PUBLICATIONChapter:SET THEORYExercise:Test Yourself
Explore 15 Videos
Similar Questions
The average score of a class of boys and girls in an examination is A . The ratio of boys and girls in the class is 3 : 1. If the average score of the boys is A+1 , the average score of the girls is A−1 (b) A−3 (c) A+1 (d) A+3
View SolutionLet the average score of a class of boys and girls in an examination be p. The ratio of boys and girls in the class is 3: 1. If the average score of the boys is (p + 1), then what is the average score of the girls?
View Solution
Knowledge Check
In a school, the ratio of boys to girls is 4:3 and the ratio of girls to teachers is 8:1. The ratio of students to teachers is:
A56:3B55:1C49:3D56:1The average score of a class of boys and girls in an examination is A . The ratio of boys and girls in the class is 3 : 1. If the average score of the boys is A+1 , the average score of the girls is A−1 (b) A−3 (c) A+1 (d) A+3
A(A−1)B(A−3)C(A+3)D(A+3)The average score of a-class of boys and girls in an examination is A. The ratio of boys and girls in the class is 3:1. If the average score of the boys is A + 1, the average score of the girls is :
AA+1BA−1CA+3DA−3
The ratio of the boys to girls in a class is 2:3. If 20% of boys leave this class, then the new ratio of boys to girls is
View SolutionThe ratio of the number of boys and the number of girl in a class is 9:11. If the number of boys is 18, then the number of girls is ____.
View SolutionThe ratio of the number of boys and the number of girl in a class is 9:11. If the number of boys is 18, then the number of girls is ____.
View SolutionStudy the given pie chart and answer the question that follows
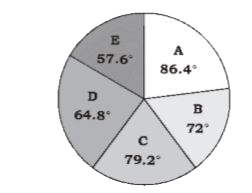
In the ratio of the number of boys to that of girls in school B is 7:6 and the ratio of the number of boys to that of girls in school D is 4 :5 then what is the ratio of the number of boys in B to that of girls in D
View SolutionThere are b boys and g girls in a class and the average of number of boys and the number of girls is 18. Then b+g=_____
View Solution
