P=b2c2−ac−bd where a, b, c and d, in that order, are four ocnsecutive natural numbers (a<b).
Which of the following statements is correct?
√P is always a prime number.
√P is always a rational number, through not necessarily prime.
√P can be rational or irretional depending on the numbers.
√P is always an irrational number.
The correct Answer is:B
To solve the problem step by step, we will evaluate the expression P=b2c2−ac−bd where a,b,c,d are four consecutive natural numbers.
Step 1: Define the consecutive natural numbers
Let’s define the four consecutive natural numbers:
- Let a=n
- Let b=n+1
- Let c=n+2
- Let d=n+3
Step 2: Substitute the values into the expression
Now we substitute a,b,c,d into the expression for P:
P=(n+1)2(n+2)2−n(n+2)−(n+1)(n+3)
Step 3: Expand the expression
Now we will expand each term:
1. Expand (n+1)2:
(n+1)2=n2+2n+1
2. Expand (n+2)2:
(n+2)2=n2+4n+4
3. Now multiply these two expansions:
(n2+2n+1)(n2+4n+4)=n4+6n3+13n2+8n+4
4. For −n(n+2):
−n(n+2)=−n2−2n
5. For −(n+1)(n+3):
−(n+1)(n+3)=−n2−4n−3
Step 4: Combine all terms
Now we combine all the terms:
P=(n4+6n3+13n2+8n+4)−(n2+2n)−(n2+4n+3)
P=n4+6n3+13n2+8n+4−n2−2n−n2−4n−3
P=n4+6n3+(13n2−2n−4n−2n)+(8n−2n−4n)+(4−3)
P=n4+6n3+11n2+2n+1
Step 5: Evaluate P for specific values of n
Let’s evaluate P for the first few values of n:
1. For n=1:
P=14+6(13)+11(12)+2(1)+1=1+6+11+2+1=21
√P=√21 (not prime)
2. For n=2:
P=24+6(23)+11(22)+2(2)+1=16+48+44+4+1=113
√P=√113 (not prime)
3. For n=3:
P=34+6(33)+11(32)+2(3)+1=81+162+99+6+1=349
√P=√349 (not prime)
Conclusion
From the evaluations, we can see that √P does not consistently yield a prime number.
Let’s define the four consecutive natural numbers:
- Let a=n
- Let b=n+1
- Let c=n+2
- Let d=n+3
Now we substitute a,b,c,d into the expression for P:
P=(n+1)2(n+2)2−n(n+2)−(n+1)(n+3)
Now we will expand each term:
1. Expand (n+1)2:
(n+1)2=n2+2n+1
2. Expand (n+2)2:
(n+2)2=n2+4n+4
3. Now multiply these two expansions:
(n2+2n+1)(n2+4n+4)=n4+6n3+13n2+8n+4
−n(n+2)=−n2−2n
−(n+1)(n+3)=−n2−4n−3
Now we combine all the terms:
P=(n4+6n3+13n2+8n+4)−(n2+2n)−(n2+4n+3)
P=n4+6n3+13n2+8n+4−n2−2n−n2−4n−3
P=n4+6n3+(13n2−2n−4n−2n)+(8n−2n−4n)+(4−3)
P=n4+6n3+11n2+2n+1
Let’s evaluate P for the first few values of n:
P=14+6(13)+11(12)+2(1)+1=1+6+11+2+1=21
√P=√21 (not prime)
P=24+6(23)+11(22)+2(2)+1=16+48+44+4+1=113
√P=√113 (not prime)
P=34+6(33)+11(32)+2(3)+1=81+162+99+6+1=349
√P=√349 (not prime)
From the evaluations, we can see that √P does not consistently yield a prime number.
Topper's Solved these Questions
- NUMBER SYSTEMBook:DISHA PUBLICATIONChapter:NUMBER SYSTEMExercise:Test Yourself
Explore 15 Videos
- NUMBER SYSTEMBook:DISHA PUBLICATIONChapter:NUMBER SYSTEMExercise:Standard Level
Explore 45 Videos
- MOCK TEST 2 Book:DISHA PUBLICATIONChapter:MOCK TEST 2 Exercise:Multiple Choice Questions
Explore 20 Videos
- PERCENTAGESBook:DISHA PUBLICATIONChapter:PERCENTAGESExercise:PRACTICE EXERCISE (TEST YOURSELF)
Explore 15 Videos
Similar Questions
Knowledge Check
For the reaction
A+B→2C+D which of the following statements is/are correct?ARate of disappearance of B = 1/2 x rate of appearance of CBRate of disappearance of B =1/2 x rate of appearance of CCRate of disappearance of A = rate of appearance of BDRate of disapperance of A = rate of disapperance of B.For the reaction of 4A+B→2C+D.. Which of the following statements is correct ?
AThe rate of formation of C and D are equalBThe rate of formation of D is one half the rate of consumption of ACThe rate of appearance of C is one half the rate of disappearance of BDThe rate of disappearance of B is one fourth of the rate of disappearance of AConsider the following structures (A),(B),(C) and (D).

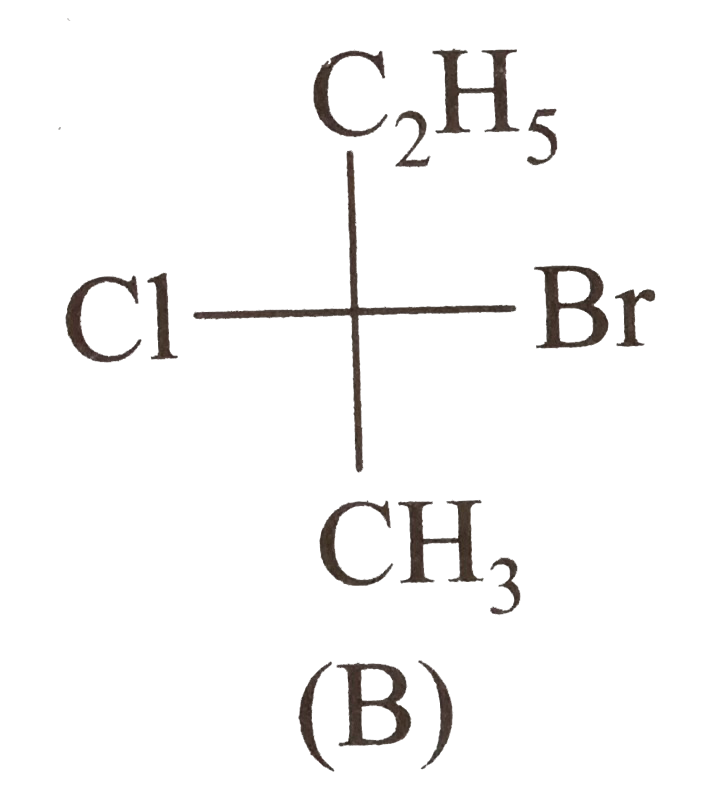

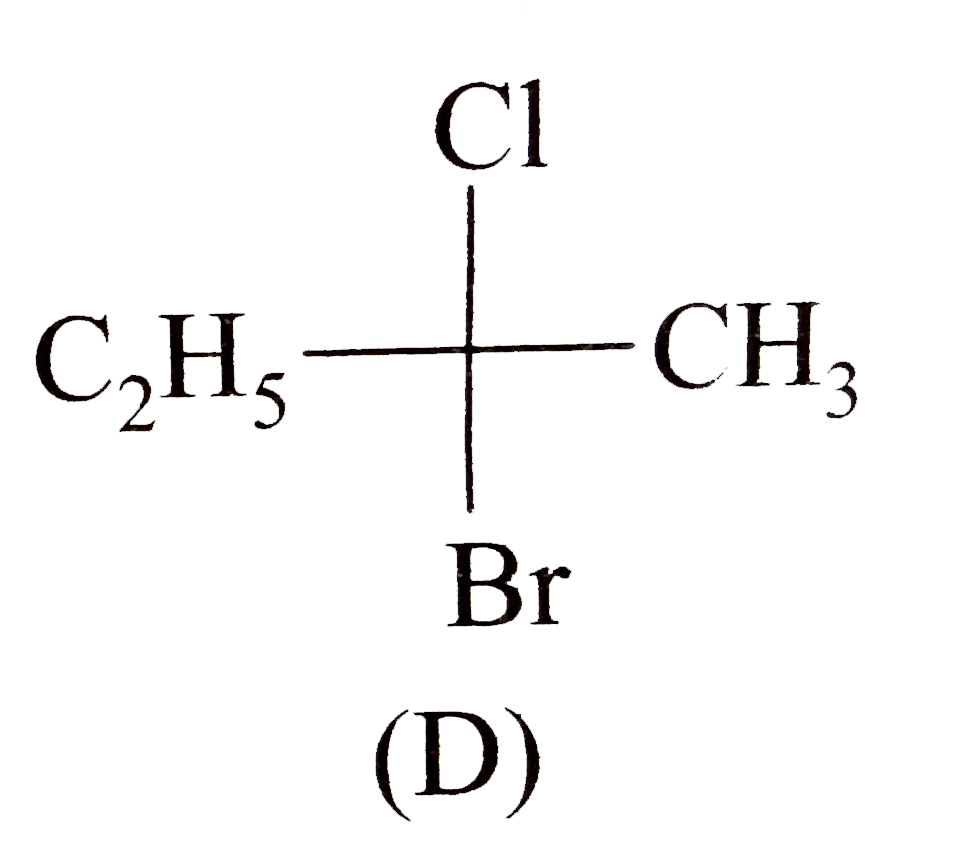
Which of the following statements is not correct?A(A)and(C) are enantiomersB(A)and(B)are enantiomersC(B)and(D)are enantiomersD(B)and(C)are identical
Consider the following statements about natural numbers: There exists a smallest natural number. There exists a largest natural number. Between two natural numbers, there is always a natural number. Which of the above statements is/are correct? None (b) Only1 (c) 1 and 2 (d) 2 and 3
View SolutionNumber of ordered triplets of natural number (a,b,c) for which abc≤11 is
View SolutionThe median BD of the triangle ABC meets AC at D. If BD=12AC , then which one of the following is correct ?
View SolutionConsider the following configurations (A),(B),(C) and (D)
(A)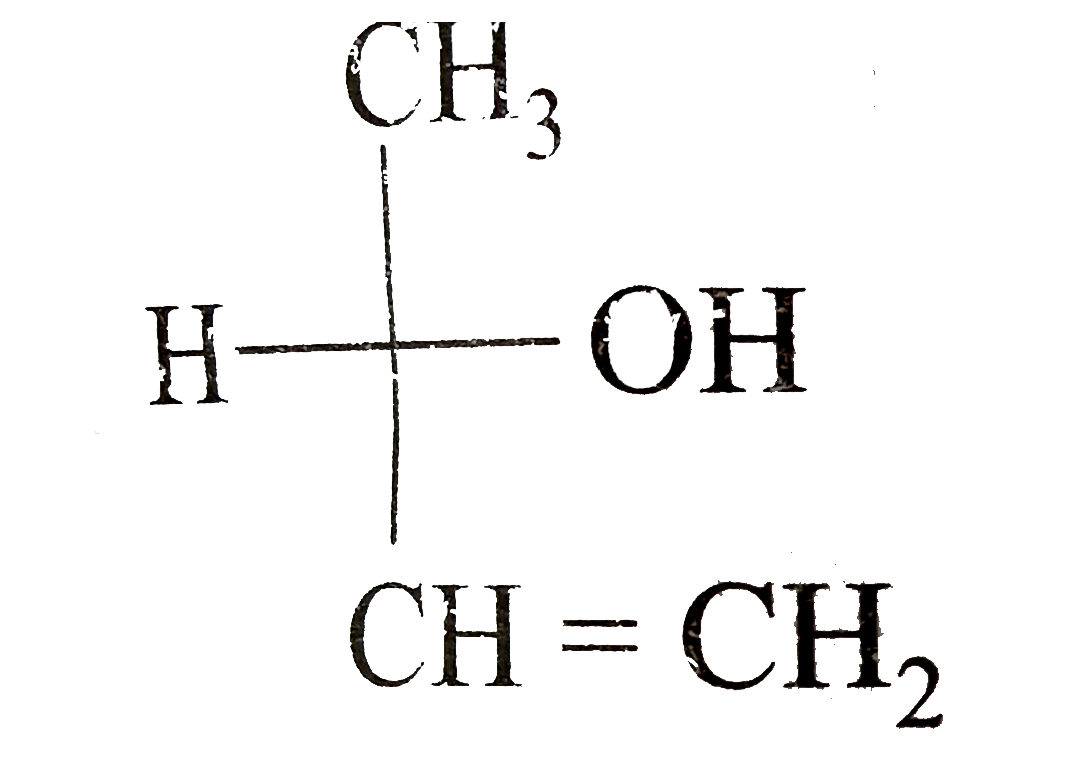
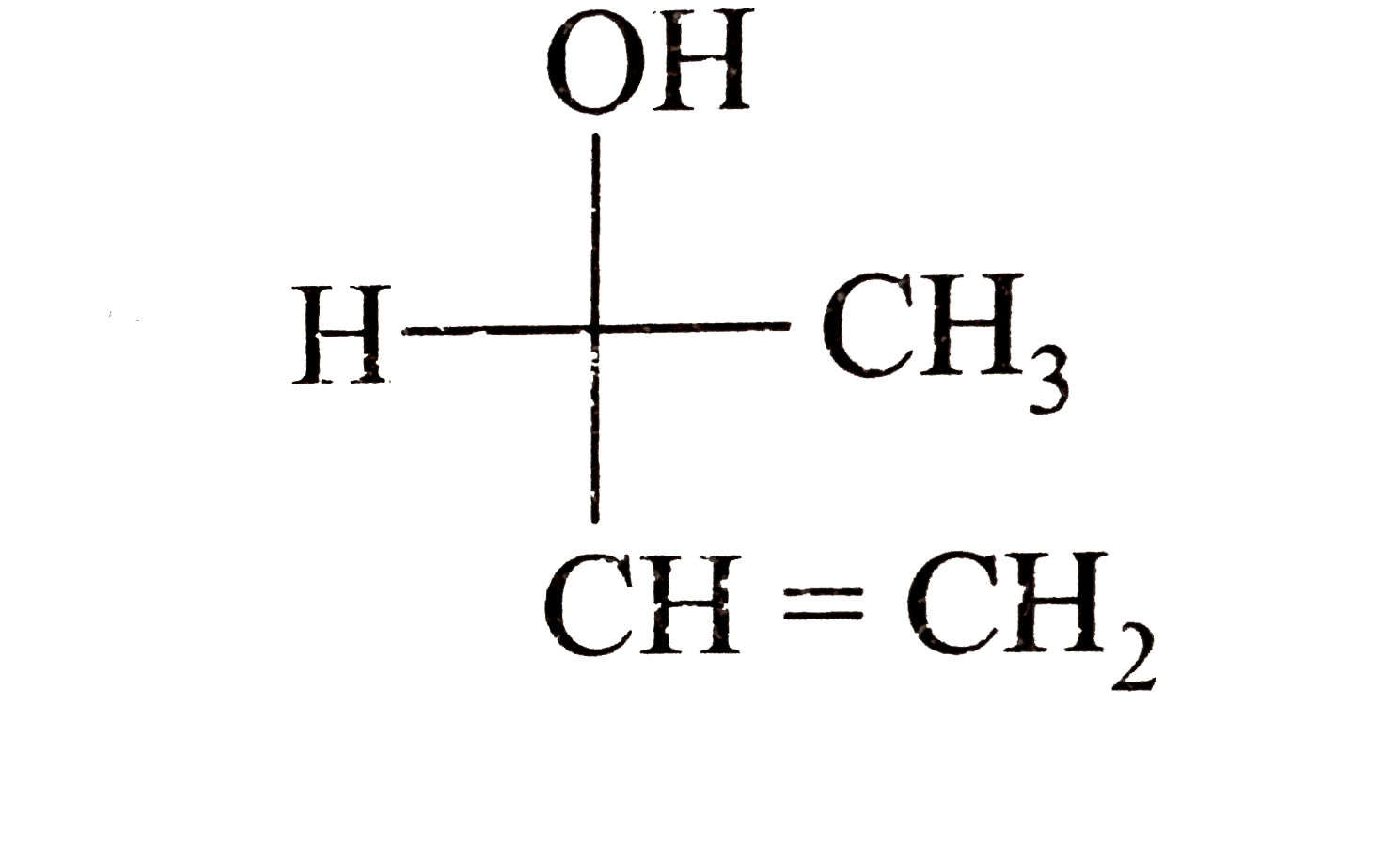
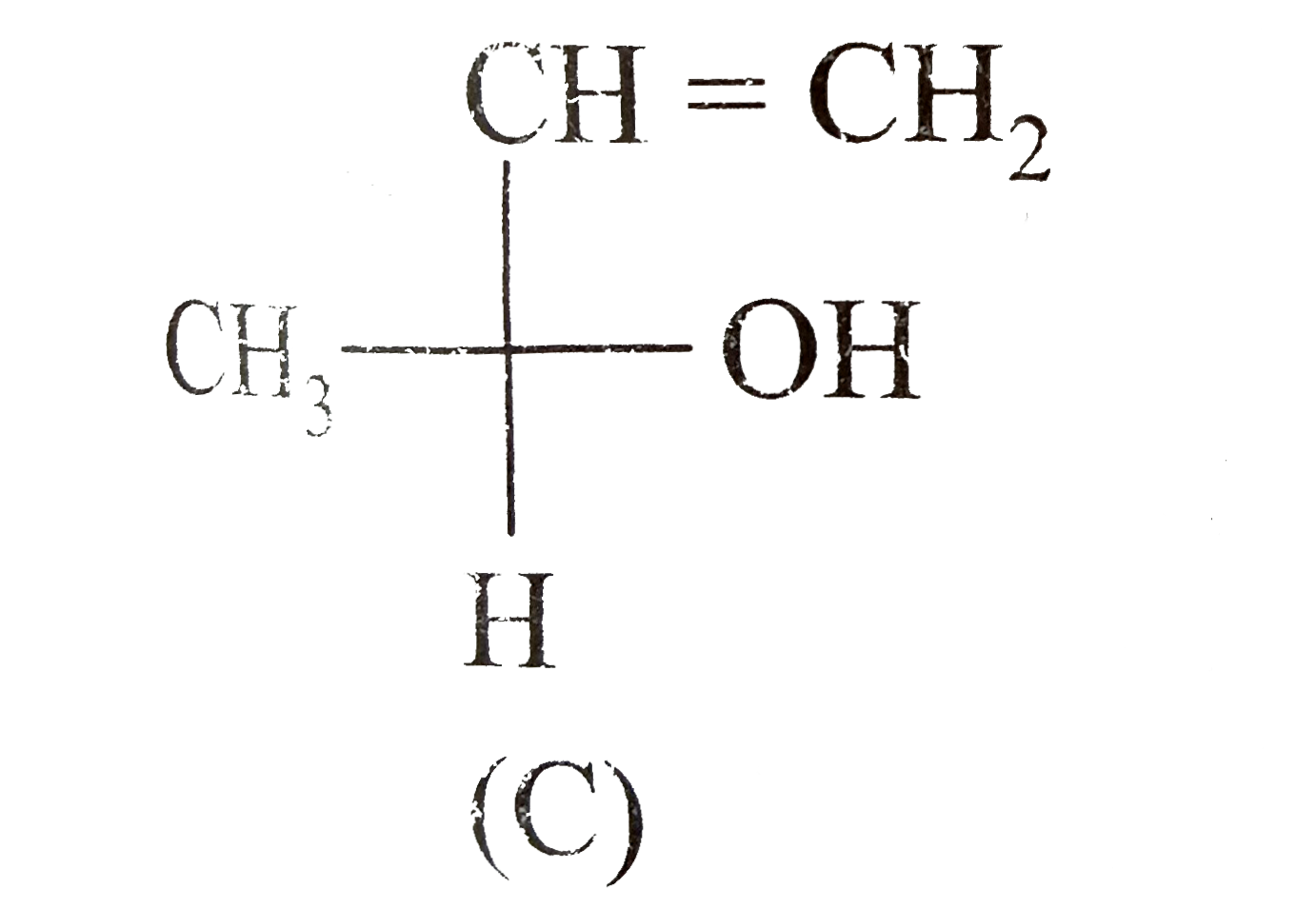
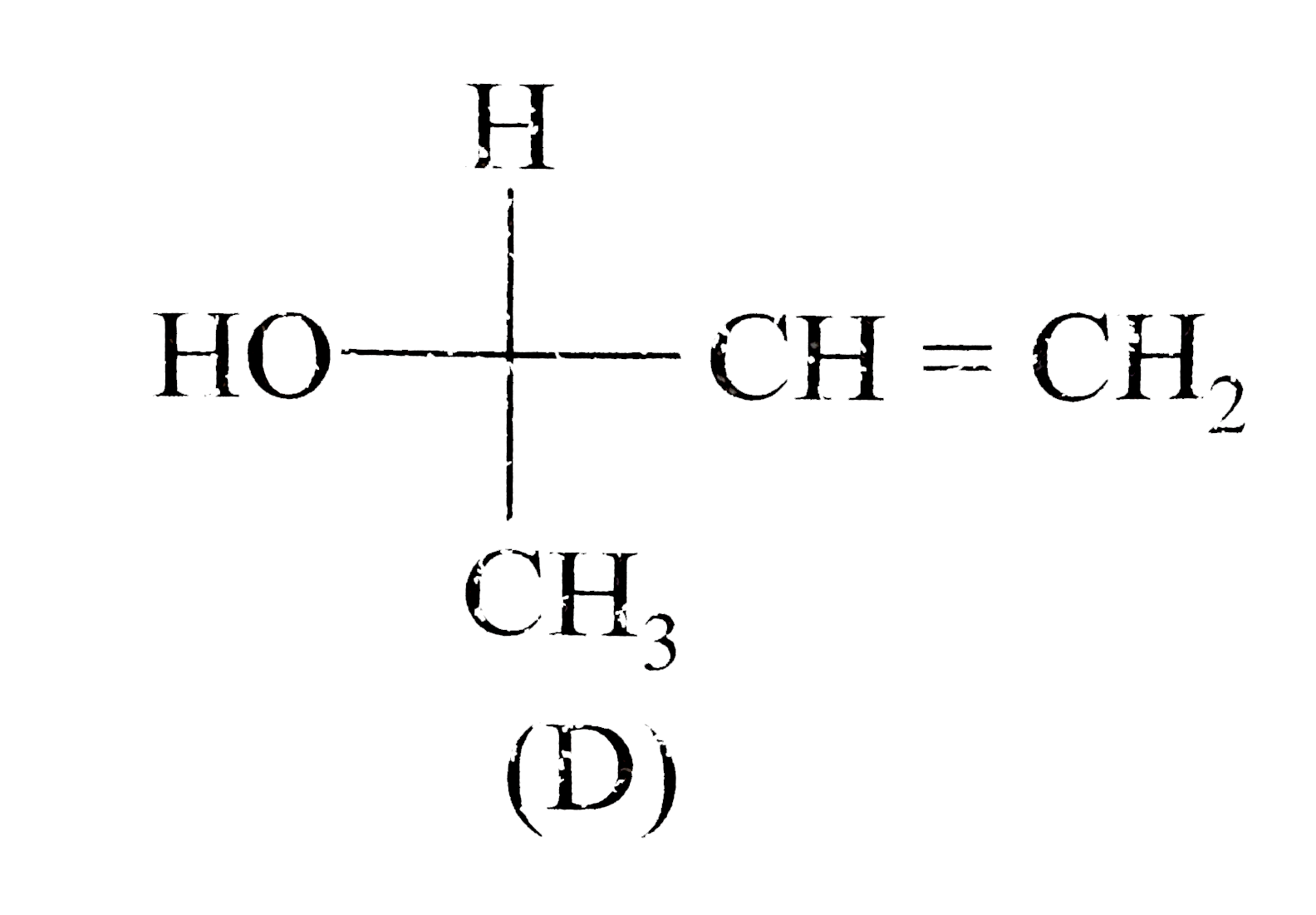
which of the following statements is not correct?
View SolutionIf a,b,c and d are four unequal positive numbers which are in A.P then
View Solution
