If p=1!+(2×2!)+(3×3!)+….+(10×10!), where n≠1×2×3×…n for integer n≥1, then p+2 when divisible by 11!, leaves a remainder
10
0
7
1
The correct Answer is:b
To solve the problem, we need to calculate the value of p given by the expression:
p=1!+2×2!+3×3!+…+10×10!
Step 1: Rewrite the terms in the sum
We can express n×n! in terms of factorials:
n×n!=n!+(n−1)×(n−1)!
This means we can rewrite each term in the sum as follows:
- 1!=1!
- 2×2!=2!+1!
- 3×3!=3!+2!
- 4×4!=4!+3!
- ...
- 10×10!=10!+9!
Step 2: Expand the sum
Now, we can expand p:
p=1!+(2!+1!)+(3!+2!)+(4!+3!)+(5!+4!)+(6!+5!)+(7!+6!)+(8!+7!)+(9!+8!)+(10!+9!)
Step 3: Combine like terms
Combining all terms, we can see that:
- Each factorial from 1! to 9! appears twice except for 10!, which appears once.
Thus, we can write:
p=2(1!+2!+3!+4!+5!+6!+7!+8!+9!)+10!
Step 4: Calculate the sum of factorials
Now, we need to compute 1!+2!+3!+4!+5!+6!+7!+8!+9!:
1!=12!=23!=64!=245!=1206!=7207!=50408!=403209!=362880
Adding these up:
1+2+6+24+120+720+5040+40320+362880=403791
Step 5: Substitute back into p
Now substituting back into the expression for p:
p=2×403791+10!=807582+3628800=4436382
Step 6: Calculate p+2
Now we calculate p+2:
p+2=4436382+2=4436384
Step 7: Find the remainder when dividing by 11!
Now we need to find 11!:
11!=39916800
Now, we calculate the remainder when 4436384 is divided by 39916800:
Since 4436384<39916800, the remainder is simply 4436384.
Final Answer
Thus, the final answer is:
The remainder when p+2 is divided by 11! is 4436384.
We can express n×n! in terms of factorials:
n×n!=n!+(n−1)×(n−1)!
This means we can rewrite each term in the sum as follows:
- 2×2!=2!+1!
- 3×3!=3!+2!
- 4×4!=4!+3!
- ...
- 10×10!=10!+9!
Now, we can expand p:
p=1!+(2!+1!)+(3!+2!)+(4!+3!)+(5!+4!)+(6!+5!)+(7!+6!)+(8!+7!)+(9!+8!)+(10!+9!)
Combining all terms, we can see that:
- Each factorial from 1! to 9! appears twice except for 10!, which appears once.
Thus, we can write:
p=2(1!+2!+3!+4!+5!+6!+7!+8!+9!)+10!
Now, we need to compute 1!+2!+3!+4!+5!+6!+7!+8!+9!:
1!=12!=23!=64!=245!=1206!=7207!=50408!=403209!=362880
Adding these up:
1+2+6+24+120+720+5040+40320+362880=403791
Now substituting back into the expression for p:
p=2×403791+10!=807582+3628800=4436382
Now we calculate p+2:
p+2=4436382+2=4436384
Now we need to find 11!:
11!=39916800
Since 4436384<39916800, the remainder is simply 4436384.
Thus, the final answer is:
The remainder when p+2 is divided by 11! is 4436384.
Topper's Solved these Questions
- NUMBER SYSTEMBook:DISHA PUBLICATIONChapter:NUMBER SYSTEMExercise:Practice Exercise (Foundation Level)
Explore 65 Videos
- NUMBER SYSTEMBook:DISHA PUBLICATIONChapter:NUMBER SYSTEMExercise:Standard Level
Explore 45 Videos
- MOCK TEST 2 Book:DISHA PUBLICATIONChapter:MOCK TEST 2 Exercise:Multiple Choice Questions
Explore 20 Videos
- PERCENTAGESBook:DISHA PUBLICATIONChapter:PERCENTAGESExercise:PRACTICE EXERCISE (TEST YOURSELF)
Explore 15 Videos
Similar Questions
Knowledge Check
Remainder when 3×722+2×1022−44 is divisible by 18 is
A16B3C12D15If 1×2×3×…….×n is denoted by
 , then
, then 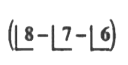 is equal to : A
is equal to : A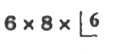 B
B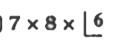 C
C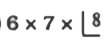 D
D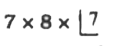
If (1×2×3×4×....×n!) = n, then (14! - 13! - 12!) is equal to
A14×12×(12!)B14×12×(13!)C14×13×(13!)D13×12×(12!)
If (1+i)(1+2i)(1+3i)...(1+ni)=a+ib then 2×5×10×....(1+n2)=
View SolutionLet P(n):2n<(1×2×3××n) . Then the smallest positive integer for which P (n) is true is
View SolutionIf n!,3×n! and (n+1)! are in G.P., then n!,5×n! and (n+1)! are in
View SolutionIf 310×272=92×3n then the value of n is
View SolutionLet P(n):2n<(1×2×3×….×n) . Then the smallest positive integers for which P(n ) is true , is
View Solution