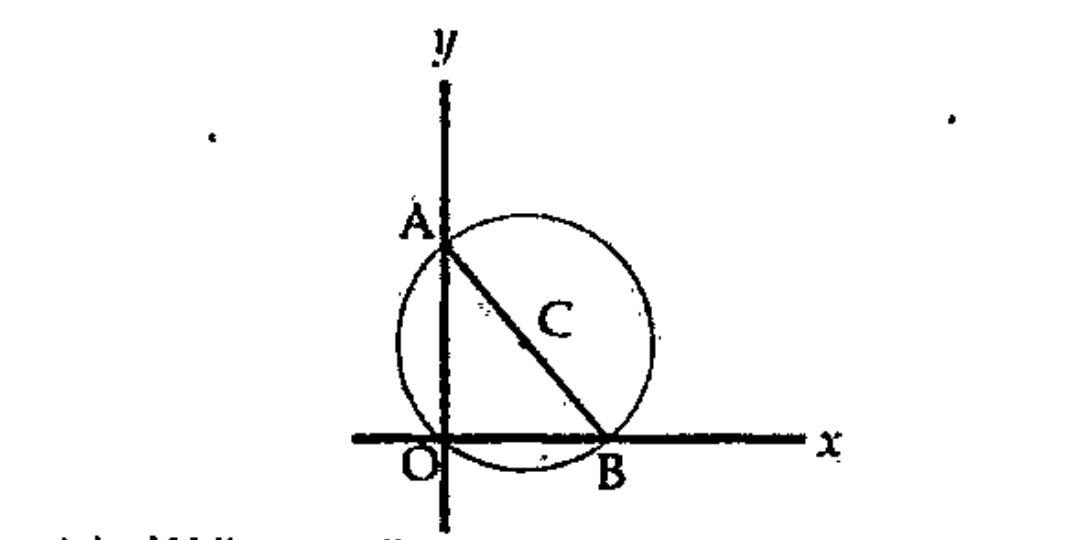
The locus of the centre of the circle which cuts a chord of length 2 a from the positive x-axis and passes through a point on positive y - axis distant b from the origin isSolution in Malayalam
x2+2by=b2+a2
x2−2by=b2+a2
x2+2by=a2−b2
x2−2by=b2−a2
The correct Answer is:C
Step by step video, text & image solution for The locus of the centre of the circle which cuts a chord of length 2 a from the positive x-axis and passes through a point on positive y - axis distant b from the origin is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A circle cuts the chord on x-axis of length 4a. If this circle cuts the y-axis at a point whose distance from origin is 2b. Locus of its centre is (A) Ellipse (B) Parabola (C) Hyperbola (D) Straight line
View SolutionFind the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.
View SolutionThe center of the circle of the circle that crosses the chord of 2a length from the positive x-axis and passes through the point on the y-axis at a distance b from the original point.
View SolutionC is the centre of the circle passing through the origin. Circle cuts the y-axis at A(0,4) and the x-axis at B(4,0).(0,0) is the point on the circle. There is one more point on the circle with x and y coordinates equal. Which is that point?
 .
.
View SolutionThe locus of the centre of the circle which cuts off intercepts of length 2a and 2b from X-axis and Y-axis respectively, is
View SolutionThe locus of the centre of circle which cuts off an intercept of constant length on the x-axis and which passes through a fixed point on the y-axis, is
View SolutionA circle is drawn to cut a chord of length 2a unit along x -axis and to touch the y-axis . The locus of the centre of the circle is :
View SolutionA circle cuts the chord on x-axis of length 4a . If this circle cuts the y-axis at a point whose distance from origin is 2b . Locus of its centre is (A) Ellipse (B) Parabola (C) Hyperbola (D) Straight line
View Solution
