x=asinωt की सरल आवर्त गति करते हुए एक कण को । x= 0 से x=2 तक विस्थापित करने में लगा समय t1 एवं x=a2 से x=a तक विस्थापित करने में लगा समय t2 हो तो अनुपात t1:t2 होगा
1:1
1:2
1:3
2:1
The correct Answer is:B
Step by step video, text & image solution for x=a sin omegat की सरल आवर्त गति करते हुए एक कण को । x= 0 से x=2 तक विस्थापित करने में लगा समय t_(1) एवं x=(a)/(2) से x=a तक विस्थापित करने में लगा समय t_(2) हो तो अनुपात t_(1):t_(2) होगा by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The velocity-time graph of a particle in one-dimensional motion is shown in Fig.
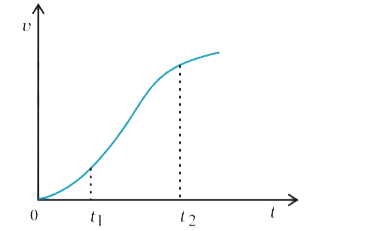
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
(a) x(t2)=x(t1)+υ(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) υ(t2)=υ(t1)+a(t2−t1)
(c ) υaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(υ(t2)−υ(t1))/(t2−t1)
(e ) x(t2)=x(t1)+υaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1)= area under the υ−t curve bounded by the t-axis and the dotted line shown.
View SolutionProve that the point of intersection of the tangents at t1andt2 on the parabola y2=4ax is (at1t2,a(t1+t2))
View SolutionA particle executes SHM of type x=Asinωt. It takes time t1 from x=0 to x=A2andt2 from x=A2 to x=A. The ratio t1:t2 will be
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View SolutionLet t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of Column I with the items Column II
Column-IColumn-IIA) x∈(0,cos1)p) t1>t2>t4>t3B) x∈(cos1,1√2)q) t4>t3>t1>t2C) x∈(1√2,sin1)r) t1>t2>t4>t3D) x∈(sin1,1)s) t3>t4>t1>t2
View SolutionLett1=(sin−1x)sin−1x,t2=(sin−1X)(cos−1x),t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of column I with the items Column II

View SolutionA particle executes SHM in accordance with x=Asinωt. If t1 is the time taken by it to reach from x=0 to x=√3(A/2)and t2 is the time taken by it to reach from x=√3/2A to x=A , the value of t1/t2 is
View SolutionLet t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x,
Match the follwing items of Column I with Column II

View Solution