The equation for pressure is
hg/d
hdg
hd/g
h/dg
The correct Answer is:B
To find the equation for pressure in a fluid, we can follow these steps:
1. Understand the Concept of Pressure:
Pressure is defined as the force exerted per unit area. In the context of fluids, pressure increases with depth due to the weight of the fluid above.
2. Identify the Variables:
- Let ρ (or D as given in the options) be the density of the liquid.
- Let g be the acceleration due to gravity.
- Let h be the height of the liquid column above the point where pressure is being measured.
3. Use the Formula for Pressure in a Fluid:
The formula for pressure at a depth h in a fluid is given by:
P=ρgh
Here, P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
4. Modify the Formula According to Given Options:
In the problem, the density is represented as D instead of ρ. Therefore, we can rewrite the pressure formula as:
P=Dgh
5. Identify the Correct Option:
From the options provided, we need to find which one matches our derived formula P=Dgh.
- The correct option is the one that states P=Dgh.
Conclusion:
The equation for pressure in a fluid at a depth h is:
P=Dgh
where D is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
---
Pressure is defined as the force exerted per unit area. In the context of fluids, pressure increases with depth due to the weight of the fluid above.
- Let ρ (or D as given in the options) be the density of the liquid.
- Let g be the acceleration due to gravity.
- Let h be the height of the liquid column above the point where pressure is being measured.
The formula for pressure at a depth h in a fluid is given by:
P=ρgh
Here, P is the pressure, ρ is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
In the problem, the density is represented as D instead of ρ. Therefore, we can rewrite the pressure formula as:
P=Dgh
From the options provided, we need to find which one matches our derived formula P=Dgh.
- The correct option is the one that states P=Dgh.
The equation for pressure in a fluid at a depth h is:
P=Dgh
where D is the density of the liquid, g is the acceleration due to gravity, and h is the height of the liquid column.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - Exercise (Match the following)5videos
THRUST AND PRESSURE
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - Exercise (Assertion & Reason type)10videos
THRUST AND PRESSURE
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - NCERT Section10videos
THRUST AND PRESSURE
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SOUNDEXERCISE - Olympiad/HOTS Corner15videos
SOUND
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - WORK AND ENERGYEXERCISE - Olympaid/HOTS Corner20videos
WORK AND ENERGY
Similar Questions
Knowledge Check
- Question 1 - Select One
The equation of displacement due to a sound wave is s=[s0sin2(ωt−kx)]if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
ABks0sin(2ωt−2kx)B−Bks0sin(2ωt−2kx)CBks0cos2(ωt−kx)D−Bks0cos2(ωt−kx) - Question 2 - Select One
The equation for Freundlich adsorption isotherm under high pressure is
Axm∝p1/nBxm∝p∘Cxm∝1pDxm∝p - Question 3 - Select One
If Z is a compressibility factor, van der Waals' equation at low pressure can be written as
AZ=1+PbRTBZ=1+RTPbCZ=1−aVRTDZ=1−PbRT
(P+av2)(v−b) = Constant. In the given equation P is pressure and v is volume. What is the unit of a?
View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
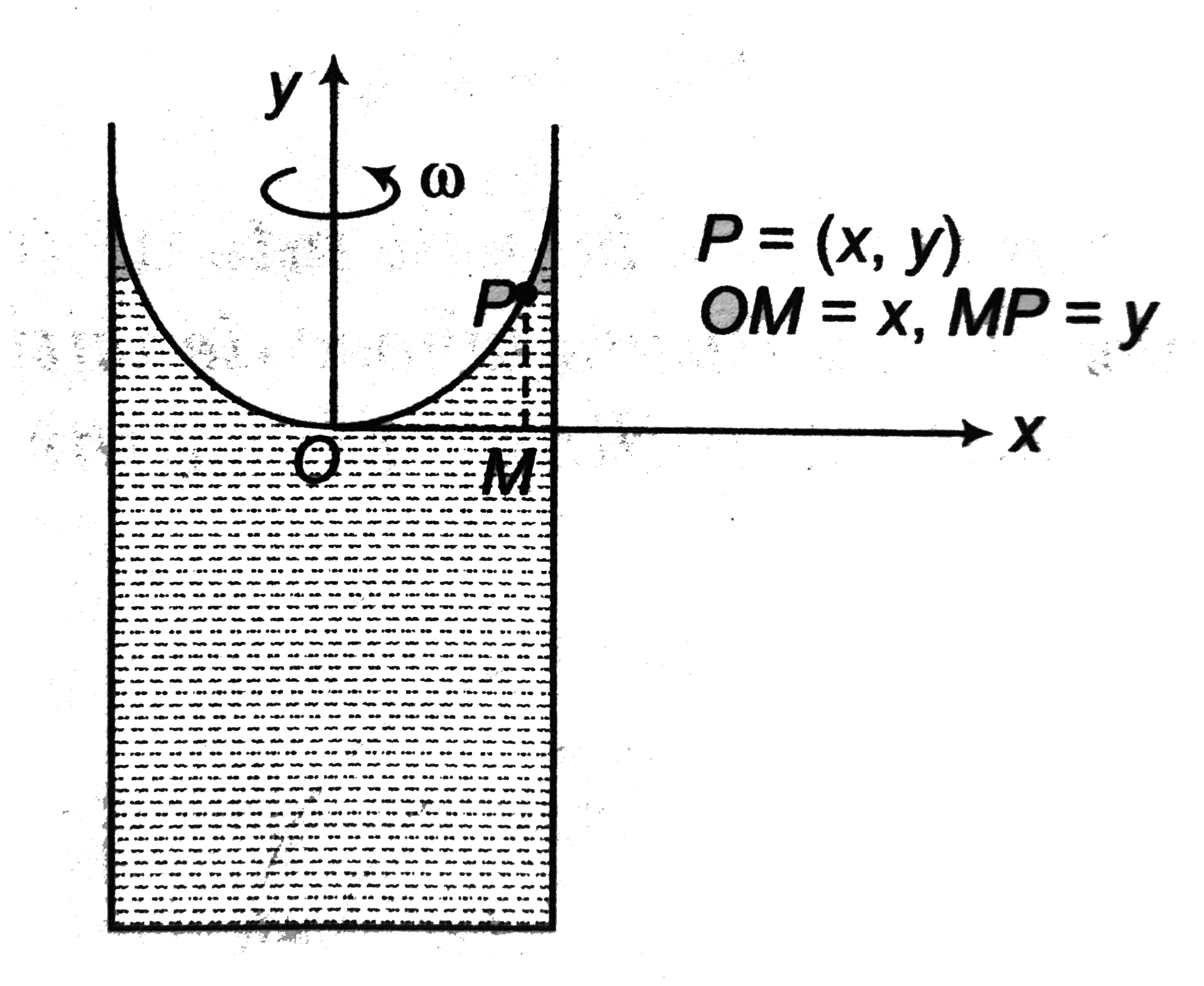.View SolutionCalculate the pressure exerted by 16 g of methane in a 250 mL container at 300 K using van der Waal's equation. What pressure will be predicted by ideal gas equation ?
a=2.253atmL2mol−2,b=0.0428Lmol−1
R=0.0821LatmK−1mol−1View SolutionIf Z is a compressibility factor, van der Waals' equation at low pressure can be written as
View SolutionIf Z is a compressibility factor, van der waals equation at low pressure can be written as
View Solution