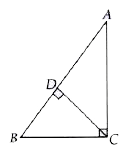
In ΔABC,m∠B=90∘,AB=4√5.BD⊥Ac,AD=4 , then area of (ΔABC) =
96 sq . Units
80 sq . Units
120 sq . Units
160 sq . Units
The correct Answer is:B
To find the area of triangle ABC, we can follow these steps:
Step 1: Understand the Given Information
- We have triangle ABC where angle B = 90°.
- AB = 4√5
- AD = 4
- BD is perpendicular to AC.
Step 2: Use the Pythagorean Theorem
Since triangle ABD is a right triangle, we can apply the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
(4√5)2=42+BD2
Step 3: Calculate the Squares
Calculating the squares:
- (4√5)2=16×5=80
- AD2=42=16
Now, substituting these values into the equation:
80=16+BD2
Step 4: Solve for BD
Rearranging the equation to find BD:
BD2=80−16
BD2=64
Taking the square root:
BD=√64=8
Step 5: Find DC Using Similar Triangles
Using the property of similar triangles (triangles ABD and BDC):
ADBD=BDDC
Substituting the known values:
48=8DC
Step 6: Cross-Multiply to Solve for DC
Cross-multiplying gives:
4⋅DC=8⋅8
4⋅DC=64
Dividing both sides by 4:
DC=644=16
Step 7: Find AC
Now, we can find AC:
AC=AD+DC=4+16=20
Step 8: Calculate the Area of Triangle ABC
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, base AC = 20 and height BD = 8:
Area=12×20×8
Step 9: Simplify the Area Calculation
Calculating the area:
Area=12×20×8=10×8=80
Final Answer
The area of triangle ABC is 80 square units.
---
- We have triangle ABC where angle B = 90°.
- AB = 4√5
- AD = 4
- BD is perpendicular to AC.
Since triangle ABD is a right triangle, we can apply the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
(4√5)2=42+BD2
Calculating the squares:
- (4√5)2=16×5=80
- AD2=42=16
80=16+BD2
Rearranging the equation to find BD:
BD2=80−16
BD2=64
Taking the square root:
BD=√64=8
Using the property of similar triangles (triangles ABD and BDC):
ADBD=BDDC
Substituting the known values:
48=8DC
Cross-multiplying gives:
4⋅DC=8⋅8
4⋅DC=64
Dividing both sides by 4:
DC=644=16
Now, we can find AC:
AC=AD+DC=4+16=20
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, base AC = 20 and height BD = 8:
Area=12×20×8
Calculating the area:
Area=12×20×8=10×8=80
The area of triangle ABC is 80 square units.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More
If a=4 then area of the ΔABC is equal to
A3√22B3C4√3D3√2 - Question 2 - Select One
If in ΔABC,∠B=90∘,AB=6√3 and AC=12cm, find BC.
A5 cmB6 cmC7 cmD8 cm - Question 3 - Select One
In ΔABC, a=12 cm, ∠B=30∘ and ∠C=90∘, then area of ΔABC=?
A6√3m2B24√3m2C36√3m2DNone of these
In ΔABC,∠ABC=150∘,AD⊥BC,AB=20cm. Find height of ΔABC.
View SolutionIn ΔABC,∠B=90∘,BD⊥AC,A−D−C. If CD=2 cm and AD=8cm then BD is equal to
View SolutionIn ΔABC, a=12 m, ∠B=30∘ and ∠C=90∘, then area of ΔABC=?
View SolutionIn ΔABC,∠ACB=90∘,AC=4andBC=3 , then the value of CD×AB is
 View Solution
View SolutionIf, in ΔABC,a=√2,b=√3,c=√5, then the area of ΔABC is
View Solution
