Two line segment AB and CD are congruent.
If AB = 6 cm, then what is the length of CD?
The correct Answer is:6 cm
To solve the problem step by step, we can follow this reasoning:
1. Understand the Concept of Congruence:
- Congruent line segments are segments that have the same length.
2. Identify the Given Information:
- We are given that the line segment AB is 6 cm long.
- We are also told that line segments AB and CD are congruent.
3. Apply the Definition of Congruence:
- Since AB and CD are congruent, this means that the lengths of AB and CD are equal.
4. Set Up the Equation:
- From the information, we can write the equation:
AB=CD
5. Substitute the Known Length:
- We know that AB=6cm.
- Therefore, we can substitute this value into our equation:
6cm=CD
6. Conclude the Length of CD:
- Hence, we find that:
CD=6cm
Final Answer:
The length of CD is 6 cm.
---
- Congruent line segments are segments that have the same length.
- We are given that the line segment AB is 6 cm long.
- We are also told that line segments AB and CD are congruent.
- Since AB and CD are congruent, this means that the lengths of AB and CD are equal.
- From the information, we can write the equation:
AB=CD
- We know that AB=6cm.
- Therefore, we can substitute this value into our equation:
6cm=CD
- Hence, we find that:
CD=6cm
The length of CD is 6 cm.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:CONGRUENCE OF TRIANGLES Exercise:Solved Examples
Explore 24 Videos
- CONGRUENCE OF TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:CONGRUENCE OF TRIANGLES Exercise:NCERT Section (Exercise 7.1)
Explore 9 Videos
- COMPARING QUANTITIES Book:MTG IIT JEE FOUNDATIONChapter:COMPARING QUANTITIES Exercise:Olympaid/HOTS Corner
Explore 20 Videos
- DATA HANDLINGBook:MTG IIT JEE FOUNDATIONChapter:DATA HANDLINGExercise:Olympiad / Hots Corner
Explore 20 Videos
Similar Questions
In the given figure, AB is a diameter of a circle and CD is perpendicular to AB, if AB = 10 cm and AE = 2 cm, then what is the length of ED ?

View SolutionTwo same circles of radius 5 cm has a direct tangent AB and a transversal CD which touch circle at A, B and C, D respectively. If CD = 24 cm then find the length of AB (in cm)?
View Solution
Knowledge Check
In the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cmIn ΔABC, the height CD intersects AB at D. The mid-points of AB and BC are P and Q respectively. If AD = 8 cm and CD = 6 cm, then the length of PQ is
A3 cmB7 cmC9 cmD5 cmIn a circle with centre P.AB and CD are congruent chords. If ∠PAB=40∘, then ∠CPD=
A40∘B80∘C100∘D50∘
Two chords, AB and CD of circle meet at a point O, outside the circle. It is given that AB =7 cm, CD = 4 cm, OB = 5 cm. what is the length of OD?
किसी वृत्त की दो जीवाएं AB और CD, वृत के बाहर बिंदु O पर मिलती है|दिया गया है कि AB =7 cm, CD = 4 cm, OB = 5 cm तो OD क लंबाई क्या है?
View SolutionGiven two line segments AB and CD with measure 4.2 cm . Now draw a line segment of length equal to sum of line segment AB and CD.
View SolutionIn Figure, if line segment AB is parallel to the line segment CD, what is the value of y? (a)12 (b) 15 (c) 18 (d) 20
View Solution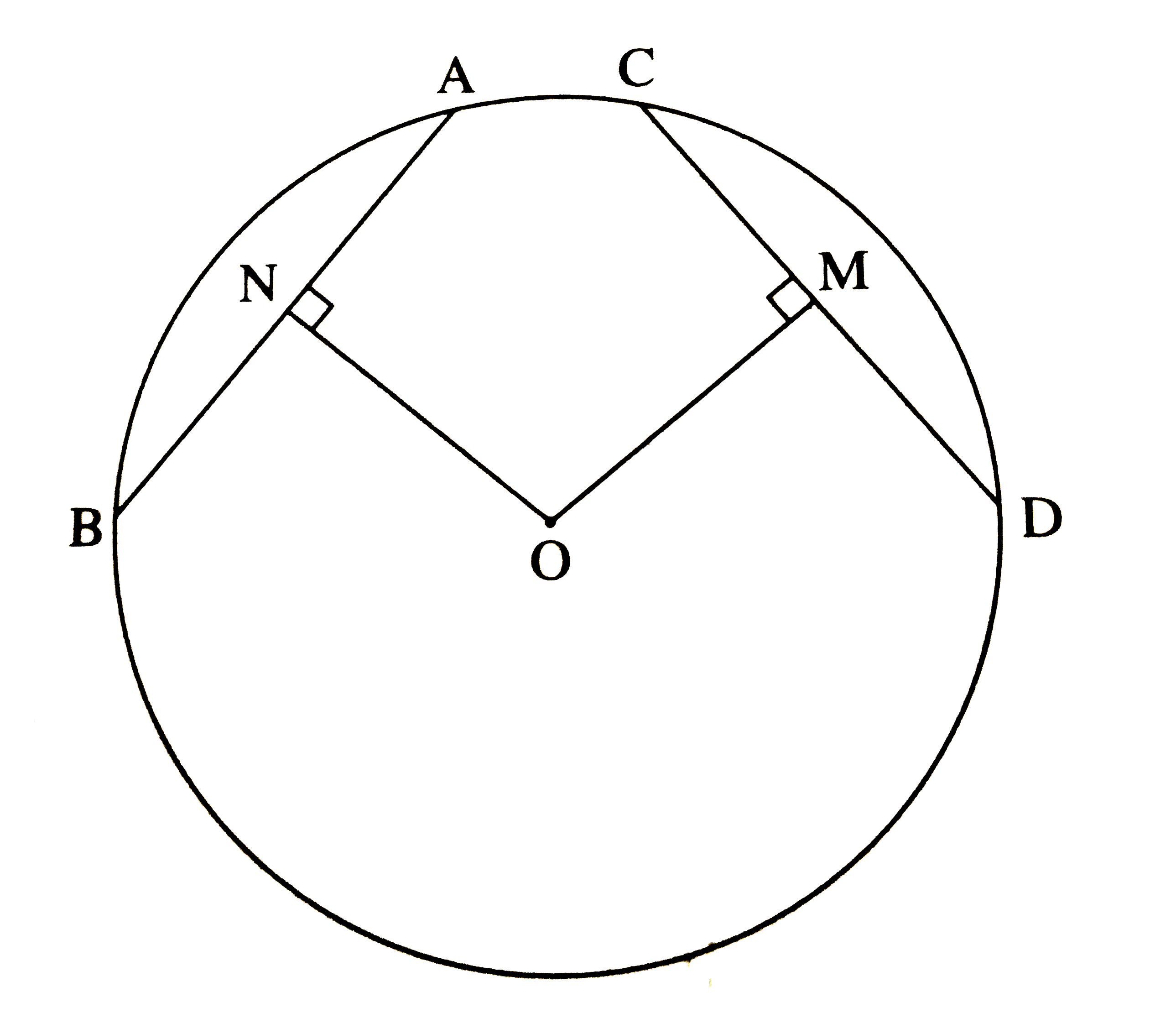
In the figure , O is the center of the circle.chord AB and CD are congruent . If seg ON ⊥ chord AB and seg OM ⊥ chord CD and OM =4cm , then find ON . Justify your answer .
View SolutionChords AB and CD of a circle interest at E and are perpendicular to each other. Segments AE, EB and ED are of lengths 2 cm, 6 cm and 3 cm respectively. Then the length of the diameter the circle in cm is :
View Solution
