Assertion : A quadrilateral has 4 and 2 angle and 4 diagonals.
Reason : A quadrilateral is a polygon made up of line segments.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.
The correct Answer is:d
To solve the assertion and reason question regarding quadrilaterals, we will analyze both statements step by step.
Step 1: Analyze the Assertion
The assertion states: "A quadrilateral has 4 angles and 4 diagonals."
- A quadrilateral is defined as a polygon with four sides.
- By definition, a quadrilateral has exactly 4 angles (one at each vertex).
- However, the assertion claims that it has 4 diagonals.
To find the number of diagonals in a quadrilateral, we can use the formula for the number of diagonals in a polygon, which is given by:
Number of diagonals=n(n−3)2
where n is the number of sides. For a quadrilateral, n=4:
Number of diagonals=4(4−3)2=4×12=2
Thus, a quadrilateral has 2 diagonals, not 4. Therefore, the assertion is false.
Step 2: Analyze the Reason
The reason states: "A quadrilateral is a polygon made up of line segments."
- A quadrilateral is indeed a polygon.
- It consists of 4 line segments (the sides of the quadrilateral).
- These line segments are typically labeled as AB, BC, CD, and DA.
Since this statement is true, we conclude that the reason is true.
Conclusion
- The assertion is false because a quadrilateral has 4 angles but only 2 diagonals.
- The reason is true because a quadrilateral is indeed a polygon made up of 4 line segments.
Final Answer
The assertion is false, and the reason is true.
---
The assertion states: "A quadrilateral has 4 angles and 4 diagonals."
- By definition, a quadrilateral has exactly 4 angles (one at each vertex).
- However, the assertion claims that it has 4 diagonals.
The reason states: "A quadrilateral is a polygon made up of line segments."
- It consists of 4 line segments (the sides of the quadrilateral).
- These line segments are typically labeled as AB, BC, CD, and DA.
- The assertion is false because a quadrilateral has 4 angles but only 2 diagonals.
- The reason is true because a quadrilateral is indeed a polygon made up of 4 line segments.
The assertion is false, and the reason is true.
Topper's Solved these Questions
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:COMPREHENSION TYPE (PASSAGE-I)
Explore 3 Videos
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:COMPREHENSION TYPE (PASSAGE-II)
Explore 3 Videos
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:MATCH THE FOLLOWING
Explore 2 Videos
- ALGEBRABook:MTG IIT JEE FOUNDATIONChapter:ALGEBRAExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- DATA HANDLING Book:MTG IIT JEE FOUNDATIONChapter:DATA HANDLING Exercise:Olympiad/HOTS Corner
Explore 10 Videos
Similar Questions
Knowledge Check
A quadrilateral has ......... diagonals.
A1B2C3D4If the diagonals of a quadrilateral bisect each other at right angles, then this quadrilateral is
Aa rectangleBa rhombusCa kiteDnone of theseThe diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
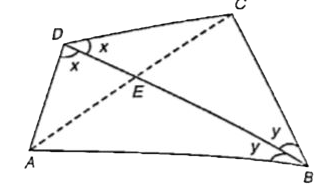 AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
A quadrilateral with each angle 90∘ and having equal diagonals is a
View SolutionA quadrilateral whose all sides, diagonals and angles are equal is a
View SolutionComplete each of the following, so as to make a true statement:
(i) A quadrilateral has ______sides.:
(ii) A quadrilateral has ______angles.:
(iii) A quadrilateral has ______vertices, no three of which are ______:
(iv) A quadrilateral has ______diagonals.:
(v) The number of pairs of adjacent angles of a quadrilateral is ______:
(vi) The number of pairs of opposite angles of a quadrilateral is ______:
(vii) The sum of the angles of a quadilateral is ______:
(viii) A diagonal of a quadrilateral is a line segment that joins two ______vertices of the quadrilateral.:
(ix) The sum of the angles of a quadrilateral is ______ right angles. :
(x) The measure of each angle of a convex quadrilateral is ______ 180 ∘ .:
(xi) In a quadrilateral the point of intersection of the diagonals lies in ______ of the quadrilateral.:
(xii) A point is in the interior of a convex quadrilateral, if it is in the ______ of its two opposite angles.:
(xiii) A quadrilateral is convex if for each side, the remaining ______ lie on the same side of the line containing the side.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angles, then this quadrilateral is a
View SolutionThe sides of a quadrilateral have lengths 2,3and4 units. If diagonals of this quadrilateral areperpendicualr to each other, the length of the fourthside can be
View Solution