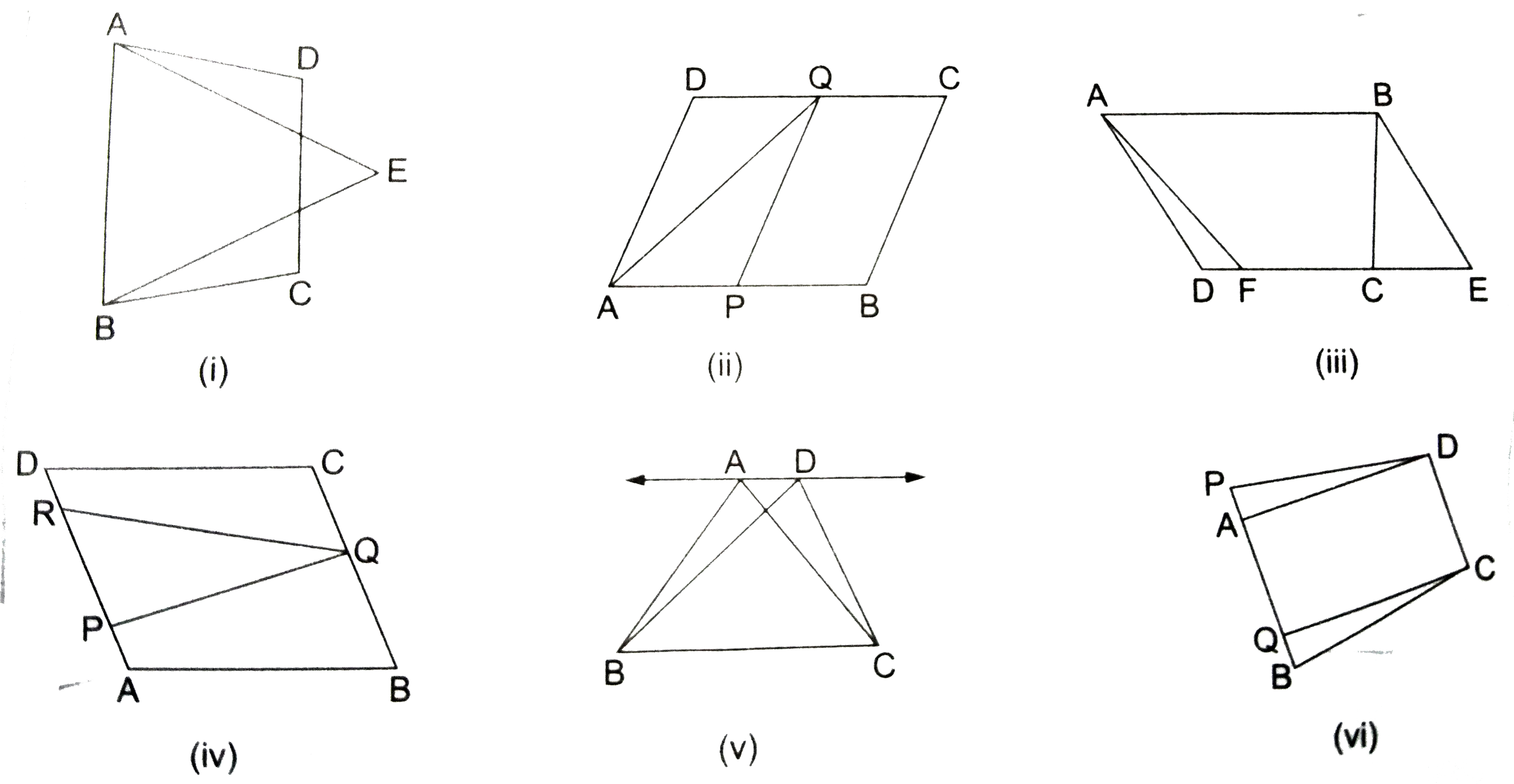
Which of the following figures lie on the same base and between the same parallels ?
A

B

C

D
all of these
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for Which of the following figures lie on the same base and between the same parallels ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )
2 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Assertion & Reason Type )
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
Knowledge Check
In which of the following figures, you find two polygons on the same base and between the same parallels?
ABCDWhich of the following figures don't have equal areas if both the figures are on same base and between same parallels ?
ATwo parallelogramsBOne parallelograms and one rectangleCTwo TrianglesDOne parallelogram and one triangleIf P, R, T are the area of a Parallelogram, a rhombus and a triangle standing on the same base and between the same parallels, which of the following is true ?
AR<P<TBP>R>TCR=P=TDR=P=2T
Out of the following given figures, which are on the same base but not between the same parallels?
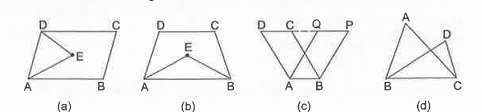
View SolutionTriangles on the same base and between the same parallel are equal in area.
View SolutionUsing vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionProve by vector method that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View Solution