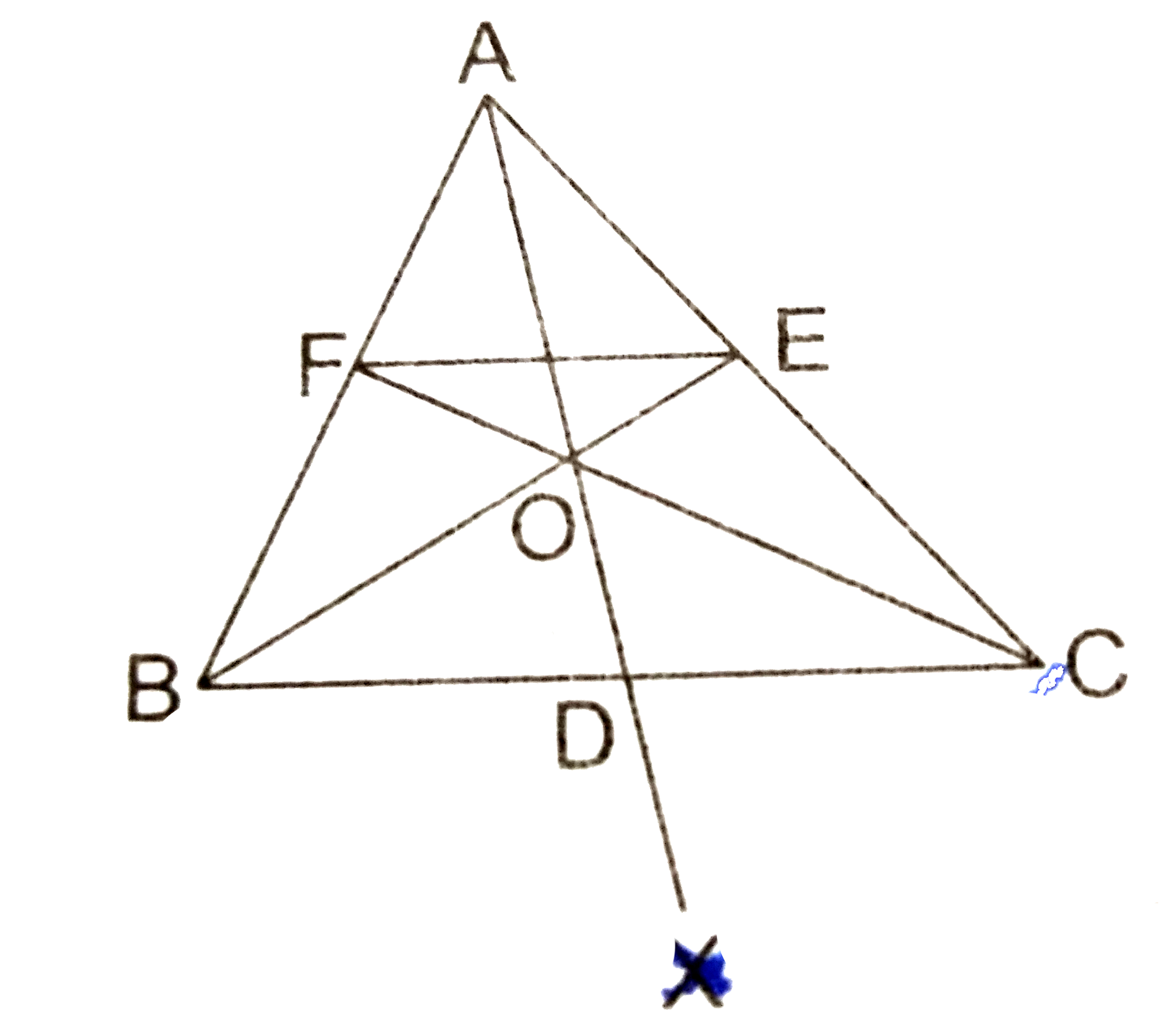
In the given figure, sid BC of ΔABC is biseted at D and O is any point AD.BO and CO produced meet AC and AB at E and F respetively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF∣∣BC.
3AC
12AC
2AC
13AC
The correct Answer is:D
Step by step video, text & image solution for In the given figure, sid BC of Delta ABC is biseted at D and O is any point AD.BO and CO produced meet AC and AB at E and F respetively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF||BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Subjective Problems) (Very Short Answer Type)
10 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Subjective Problems) (Short Answer Type)
5 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Comprehension Type PASSAGE-II )
3 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In the given figure, side BC of ΔABC is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that AO:AX=AF:AB and show that EF∣∣BC.

View SolutionThe side BC of a triangle ABC is bisected at D;o is any point in AD,BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FEBC.
View SolutionThe side BC of a ΔABC is bisected at D. O is any point on AD, BO and CO are produced to meet AC and AB at E and F respectively and AD is produced to G so that D is the midpoint of OG. Prove that FE∣∣BC
View SolutionThe side BC of a ΔABC is bisected at D. O is any point on AD. BO and CO are produced to meet AC and AB at E & F respectively. AD is produced to C1 so that D is the mid-point of OC1. Prove that FE||BC.
View SolutionIn a triangle ABC, AD is the median through A and E is the midpoint of AD, and BE produced meets AC at F. Then AF is equal to
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionIn ΔABC, E is the midpoint of the median AD. BE produced meets AC at F. Prove that AF=(13)AC
View Solution
