The total number of biodegradable materials among the following is ________ .
metallic can, peels of orange, aluminium wire, newspaper cuttings, tyre, plastic ball
The correct Answer is:2
To determine the total number of biodegradable materials from the list provided, we need to analyze each item based on whether it can be broken down by natural processes, particularly by bacteria.
1. Identify the materials: The items given in the question are:
- Metallic can
- Peels of orange
- Aluminium wire
- Newspaper cuttings
- Tyre
- Plastic ball
2. Evaluate each material:
- Metallic can: This is made of metal and does not biodegrade. (Not biodegradable)
- Peels of orange: This is organic waste and can be broken down by bacteria. (Biodegradable)
- Aluminium wire: Like the metallic can, aluminium does not biodegrade. (Not biodegradable)
- Newspaper cuttings: Made from paper, which is organic, and can be decomposed by bacteria. (Biodegradable)
- Tyre: Made from rubber, tyres are not biodegradable and can take a long time to decompose. (Not biodegradable)
- Plastic ball: Plastic is synthetic and does not decompose easily. (Not biodegradable)
3. Count the biodegradable materials:
- From the evaluation, the biodegradable materials identified are:
- Peels of orange
- Newspaper cuttings
- Therefore, there are a total of 2 biodegradable materials.
Final Answer:
The total number of biodegradable materials among the following is 2.
---
- Metallic can
- Peels of orange
- Aluminium wire
- Newspaper cuttings
- Tyre
- Plastic ball
- Metallic can: This is made of metal and does not biodegrade. (Not biodegradable)
- Peels of orange: This is organic waste and can be broken down by bacteria. (Biodegradable)
- Aluminium wire: Like the metallic can, aluminium does not biodegrade. (Not biodegradable)
- Newspaper cuttings: Made from paper, which is organic, and can be decomposed by bacteria. (Biodegradable)
- Tyre: Made from rubber, tyres are not biodegradable and can take a long time to decompose. (Not biodegradable)
- Plastic ball: Plastic is synthetic and does not decompose easily. (Not biodegradable)
- From the evaluation, the biodegradable materials identified are:
- Peels of orange
- Newspaper cuttings
- Therefore, there are a total of 2 biodegradable materials.
The total number of biodegradable materials among the following is 2.
Topper's Solved these Questions
- FOOTSTEPS TOWARDS (JEE MAIN)Book:MTG IIT JEE FOUNDATIONChapter:FOOTSTEPS TOWARDS (JEE MAIN)Exercise:SECTION B (NUMBERIC VALUE TYPE QUESTIONS)
Explore 10 Videos
- COMBUSTION AND FLAME Book:MTG IIT JEE FOUNDATIONChapter:COMBUSTION AND FLAME Exercise:OLYMPIAD/HOTS CORNER
Explore 15 Videos
- FOOTSTEPS TOWARDS (NEET)Book:MTG IIT JEE FOUNDATIONChapter:FOOTSTEPS TOWARDS (NEET)Exercise:Multiple Choice Question
Explore 45 Videos
Similar Questions
The total number of amines among the following which can be synthesized by Gabriel synthesis is ______
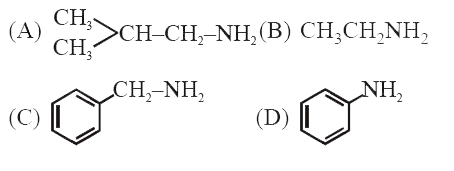
View Solution(a) What is meant by biodegradable waste materials ? Give two examples of biodegradable wastes.
(b) Which of the following materials are non- biodegradable?
Aluminium wire, Tea leaves, Synthetic fibre, Wool
View Solution
Knowledge Check
The total number of ways in which 5 balls of differ- ent colours can be distributed among 3 persons so that each person gets atleast one ball is
A75B150C210D243The total number of ways in which 5 balls of different colours can be distributed among three persons so that each person gets at least one ball is :
A75B150C210D243The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is
A75B150C210D35−(3C1×25−3C2)
The number of materials from the given list which can be used to make cooking utensils is wood , plastic , glass , clay, steel , iron , aluminium , brass , rubber .
View SolutionAmong the following fin out the total number of black metal sulphides.
CuS,NiS,CoS,ZnS,CdS
View SolutionCategorize the materials of the following products into 'can be recycled' and 'cannot be recycled Telephone instruments, plastic toys, cooker handles, carry bags, ball point pens, plastic bowls, plastic covering on electrical wires, plastic chairs, electrical switches
View SolutionThe total number of ways in which 5 balls of differert colours can be distributed among 3 persons so thai each person gets at least one ball is
View SolutionThe total number of ways in which 5 balls of differ- ent colours can be distributed among 3 persons so that each person gets atleast one ball is
View Solution
