Discuss the motion of charged particle in uniform magnetic field, when its moves at an angle $θ$ with the direction of magnetic field. Prove that its path is helical. Calculate the pitch of helical path. What will be the nature of path if $θ = 90^{\circ}$ Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

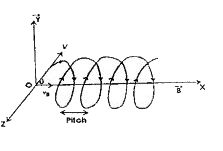
Let at any instant particle is moving with velocity v inside the uniform magnetic field $\to B$ making an angle $θ$ with the direction of magnetic field.
Resolve $\to v$ into two rectangular components
(i) $v_{B} = v cos θ =$ the component of $\to v$ along the direction of magnetic field.
(ii) $v_{n} = v cos θ =$ the component of velocity $\to v$ normal to the direction of magnetic field.
As the magnetic field act perpendicular to the velocity component $v_{n}$ , the charged particle moves along a circular path.

As centripetal force is provided by magnetic force
$∴ B q v_{n} = \frac{m v_{n}^{2}}{r}$ [ $v_{n}$ is responsible for their motion in circular path]
$r = \frac{m v_{n}}{B q} = \frac{m v sin θ}{B q} ... (i)$
The period of the circular path is given by
$T = \frac{2 π r}{v_{n}} = \frac{2 π}{v sin θ} \times \frac{m v sin θ}{B q}$
or $T = \frac{2 π m}{B q} ... (i i)$
As the charged particle moves along circular path in XY-plane due to the velocity component $v_{n}$ , it also advances linearly along OZ due to the velocity component $v_{B}$ . As a result, the charged particle will move along the path as shown in Fig. Such a path is called helical path.
Pitch : The distance travelled by the charged particle. along the direction of magnetic field in a time it completes one revolution. is called pitch of the helical path. Therefore
Pitch of the helical path $= v_{B} \times T = v cos θ \times \frac{2 π m}{B q}$
Pitch $= \frac{2 π m v cos θ}{B q}$
Pitch of the helical path is equal to the spacing between its two consecutive circular paths
(i) if $θ = 90^{\circ}$ i.e., when charged particle moves in a direction perpendicular to the direction of magnetic field $(\to B)$ then
$r = \frac{m v sin 90}{B q}$
$r = \frac{m v}{B q}$
$v_{B} = v {cos 90}^{\circ} = 0$
It means that charged particle moves in a circular path.
(ii) If $θ = 180^{\circ}$ then F $F = B q v {sin 180}^{\circ} = 0$ . Magnetic force acting on the charged particle ix zero and hence it will continue to move along the same path antiparallel to $\to B$ with same velocity $\to v$ .

Updated on:21/07/2023

|

Class 12 PHYSICS FORCE ON A CHARGE

Topper's Solved these Questions

Similar Questions

BETTER CHOICE PUBLICATION-FORCE ON A CHARGE -LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile