At room temperature, sodium crystallizes in a body-centred cubic lattice with a=4.24 Å, calculate theoretical density of sodium in g cm−3 (atomic mass of Na=23).Solution in Malayalam
A body-centred cubic unit cell contains 8 atoms at the 8 corners and one in the centre
∴ Total number of atoms per unit cell=8×18+1=2
∴Density=n×atomic massAv.no.×a3=2×236.02×1023×(4.24×10−8)3=1.002g cm−3
Topper's Solved these Questions
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-3 (Statement Type)
5 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-3 (Linked Comprehension Type)
10 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-3 (Matching Column Type)
5 Videos
- REDOX REACTION & ELECTROCHEMISTRYBOOK - BRILLIANT PUBLICATIONCHAPTER - REDOX REACTION & ELECTROCHEMISTRYEXERCISE - QUESTION (ELECTROCHEMISTRY) (LEVEL -II) (ASSERTION-REASON)
3 Videos
- SOLUTIONSBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLUTIONSEXERCISE - Level-III (Linked Comprehension Type)
12 Videos
Similar Questions
Statement 1: In crystal lattice, the size of the tetrahedral void is larger than an octahedral void.
Statement 2: The cations occupy less space than anions in crystal packing.
View SolutionF centre is an example of metal excess defect due to the presence of extra cations at interstitial sites. Zinc oxide is white in colour at room temperature, on heating it loses oxygen and turns yellow.
ZnOHeat−−→Zn2++12O2+2e−
Now there is excess of zinc in the crystal and its formula becomes Zn1+x O. the excess of Zn2+ ions move to interstitial sites and the electrons to neighbouring interstitial sites.
There are many solids which are difficult to prepare in the stiochiometric composition and contain less amount of the metal as compared to stiochiometric proportion. a typical example of this type is FeO which is mostly found with a composition of Fe0.95. it may actually range from Fe0.96 O.
Q. In Fe0.95 O:
View SolutionMatch the crystal systems/unit cells mentioned in Column I with their characteristic features mentioned in Column II.
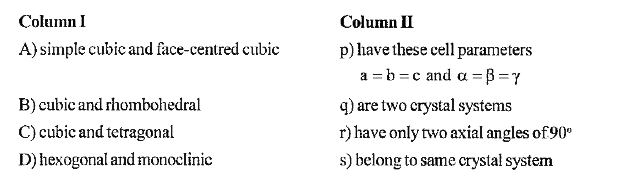
View SolutionAssertion: After the electrolysis of aqueous CuSO4 solution pH decreases.
Reason: Sulphuric acid is formed.
View Solution1 mole of A and 1 mole B are mixed together to form an ideal solution at 25∘C. Solution is placed in a vessel fitted with piston. If pressure on the solution is reduced isothermally.
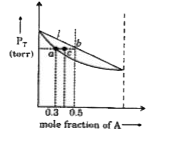
Correct relationship between P∘AandP∘B is
View SolutionAt room temperature, sodium crystallized in a body - centred cubic lattrice with a=4.24Å . Calculate theoretical density of sodium ( at wt. of Na =23) .
View SolutionSodium crystallises in a cubic lattice and the edge length of the unit cell is 430 pm. Calculate the number of atoms in the unit cell. (Atomic mass Na = 23 amu, Density of Na = 0.9623 g cm−3)
View SolutionSodium metal crystallises in body centred cubic lattic with cell edge 4.29 Å .What is the radius of sodium atom ?
View Solutionसामान्य ताप पर Na bcc जालक में क्रिस्टलीकृत होता है जिसके लिए a = 4.24 Å | Na के घनत्व का सैध्दांतिक मान है : (Na = 23)
View SolutionSodium metal crystallises in body centred cubic lattic with cell edge 4.29Å .What is the radius of sodium atom ?
View SolutionSodium (atomic mass = 23) forms face-centred cubic crystal. What is the density of sodium crystal if the radius of sodium atom is 1.91Å?
View SolutionAt room temperature, sodium crystallises in a body centred cubic cell with a = 4.24 Å. The theoretical density of sodium is –( Atomic mass of sodium = 23.0 g mol–1)
(A) 2.05 g cm–3 (B) 3.45 gcm–3
(C) 1.00 g cm–3 (D) 3.55 g cm–3
View Solutionसोडियम का क्रिस्टलन अतः केंद्रित घनीय(bcc) जालक मे होता हैं। 1 ग्राम सोडियम मे एकक कोष्ठिकाओं की संख्या लगभग कितनी होगी की गणना कीजिये यदि Na का परमाणु द्रव्यमान 23 u हैं।
View SolutionSodium metal crystallises in a body-centred cubic lattice with the cell edge, 'a' = 4.29 Å . The radius of the Na-atom will be
View SolutionSodium metal crystallizes in a body centred cubic lattice with a unit cell edge of 4.29 Å. The radius of sodium atom is approximately :
View SolutionSodium crystallizes in a face centred cubic lattice. The approximate number of unit cells in 5.0 g of sodium is (Atomic mass of sodium = 23 amu)
View Solution
