Let '*' be the binary operation defined on R by a*b = 1 + ab ∀a,b∈R
neither commutative nor associative.Solution in Punjabi
Step by step video & image solution for Let '*' be the binary operation defined on R by a*b = 1 + ab AA a,binR neither commutative nor associative. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBook:MODERN PUBLICATIONChapter:RELATIONS AND FUNCTIONExercise:EXAMPLE
Explore 212 Videos
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:EXERCISE
Explore 543 Videos
- RELATIONS AND FUNCTIONSBook:MODERN PUBLICATIONChapter:RELATIONS AND FUNCTIONSExercise:EXAMPLE
Explore 13 Videos
Similar Questions
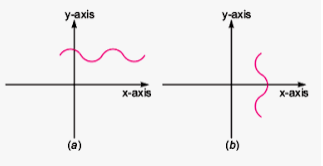
Which one of the following graph represents the function of x? Why?
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View SolutionLet * be a binary operation on R defined by a⋅b=ab+1 . Then, * is commutative but not associative associative but not commutative neither commutative nor associative (d) both commutative and associative
View SolutionLet * be a binary operation on N defined by a*b = ab for all a,b ∈ N show that * is neither commutative nor associative
View SolutionDefine * on Z by a*b =a-b+ab
show that * is a binary operation operation on z which is neither commutative nor associative
View SolutionProve that the binary operation ∘ defined on Q by a∘b=a−b+ab for all a,b in Q is neither commutative nor associative.
View SolutionAn operation ∗ on Z, the set of integers, is defined as, a∗b=a−b+ab for all a,b∈Z. Prove that ∗ is a binary operation on Z which is neither commutative nor associative.
View SolutionLet * be a binary operation on Q, defined by a * b =ab2,∀a,b∈Q. Determine whether * is commutative or associative.
View Solutionपरिमेय संख्याओं के समुच्चय Q में एक द्विआधारी संक्रिया *,a * b = a−b2 से परिभाषित है । कि संक्रिया * न तो क्रमविनिमेयी है और न ही साहचर्यी है।
View SolutionLet * be a binary operation on R defined by a⋅b=ab+1 . Then, * is commutative but not associative associative but not commutative neither commutative nor associative (d) both commutative and associative
View SolutionLet * be a binary operation on R defined by a*b= ab+1 . Then, * is (a)commutative but not associative (b)associative but not commutative (c)neither commutative nor associative (d) both commutative and associative
View SolutionLet ∗ be the binary operation defined on Q. Find which of the following binary operations are commutative.
a∗b=a+ab,∀a,b∈Q
View SolutionIf ∗ be binary operation defined on R by a∗b=1+ab,∀a,b∈R . Then the operation ∗ is
(i) Commutative but not associative.
(ii) Associative but not commutative .
(iii) Neither commutative nor associative .
(iv) Both commutative and associative.
View SolutionLet ∗ be the binary operation on Q define a∗b=a+ab. Is ∗ commutative ? Is ∗ associative ?
View SolutionOn the set R of real numbers, a binary operation o is defined by a0b=a+b+a2b ∀a,b∈R. Prove that the operation is neither commutative nor associative.
View Solution

