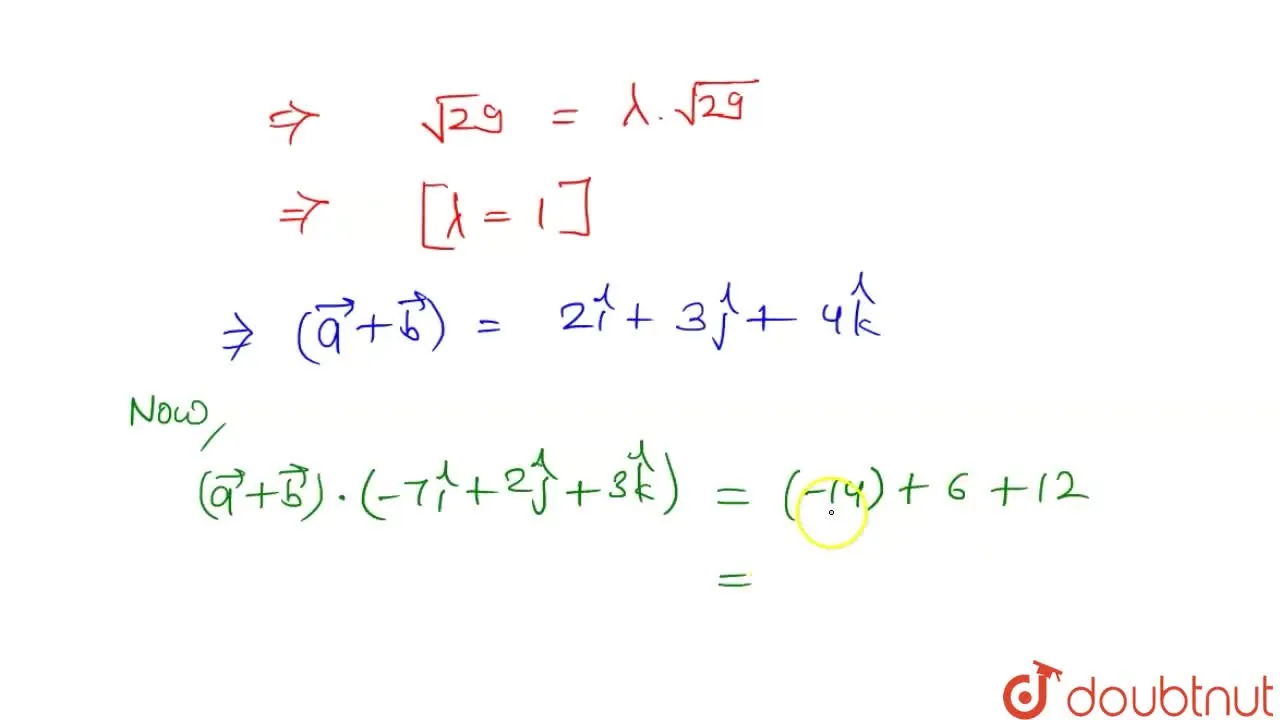IF a and b are vectors such that and , then a possible value of is
The correct Answer is:C
4
Related Playlists
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Self Assessment Test (Assertion/Reason )1videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Self Assessment Test (Comprehension)3videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Problem Set (4) (MULTIPLE CHOICE QUESTIONS)8videos
ADDITION AND MULTIPLICATION OF VECTORS
- BOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST16videos
AREA OF CURVES
Similar Questions
If aandb are vectors such that |a+b|=√29anda×(2i+3j+4k)=(2i+3j+4k)×b, then a possivalue of (a+b)⋅(−7i+2j+3k) is
View SolutionIf →aand→b are vectors such that ∣∣→a+→b∣∣=√29and→a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b , then a possible value of (→a+→b).(−7ˆi+2ˆj+3ˆk) is
View SolutionIf →a and →b are vectors such that ∣∣→a+→b∣∣=√29 and →a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)×→b, then a possible value of (→a+→b)⋅(−7→i+2ˆj+3^) is
View SolutionIf a and b are vectors in space given by a=ˆi−2ˆj√5andb=2ˆi+ˆj+3ˆk√14, then the value of (2a+b)⋅[(a×b)×(a−2b)] is
View SolutionIf ¯a and ¯b are vectors such that ∣∣¯a+¯b∣∣=√29 and ¯a×(2¯i+3¯j+4¯k)=(2¯i+3¯j)ׯb. Possible value of (¯a+¯b)⋅(−7¯i+2¯j+3¯k) is
View SolutionIf ¯a and ¯b are vectors such that ∣∣¯a+¯b∣∣=√29 and ¯a×(2ˆi+3ˆj+4ˆk)=(2ˆi+3ˆj+4ˆk)ׯb then the value of (¯a+¯b).(−7ˆi+2ˆj+3ˆk) is .......
View SolutionIf a=1√10(3i+k) and b=17(2i+3j−6k), then the value of (2a−b).[(a×b)×(a+2b)] is
View SolutionIf a=2i+j+2k,b=5i−3j+k, then orthogonal projection vector of a and b is :
View SolutionIf a=i+2j−3k,b=3i−j+2k, then angle between a + b and a - b is :
View SolutionIf →a=i+j+k and →b=j−k then find vector c, such that a×c=b and a.c=3
View Solution