Derive an expression for average power in RLC circuit.
Let the alternating e.m.f. applied ot an RLC circuit be
E=E0sinωt
If alternating current developed lags behind the applied e.m.f. by a phase angle ϕ, then
I=I0sin(ωt−ϕ)
dWdt=EI
dWdt=E0sinωt×I0sin(ωt−ϕ)
dWdt=E0I0sinωt(sinωtcosϕ−cosωtsinϕ)
[∵sin(A−B)=sinAcosB−cosAsinB]
dWdt=I0E0sin2ωtcosϕ−E0I0sinωtsinϕ
dWdt=E0I0sin2cosϕ−E0I022sinωtcosωtsinϕ
dW=E0I0sin2ωtcosϕdt−E0I02sin2ωtsinϕdt
Total work done W is given by,
W=∫dW
W=T∫0E0I0sin2ωtcosϕdt−T∫0E0I02sin2ωtsinϕdt
W=E0I0cosϕT∫0sin2ωtdt−E0I02sinϕT∫0sin2ωtdt .....(1)
But T∫0sin2ωtdt=T2 and T∫0sin2ωtdt=0 ......(2)
Put (2) in (1)
∴W=E0I0cosϕT2−E0I02sinϕ(0) .....(1)
W=E0I0cosϕT2
∴Pav=WT
=E0I0cosϕT2T=E0I02cosϕ
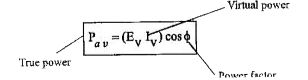
Similar Questions
Derive an experssion for the average power in LCR circuit connected to a.c. supply. Hence define power factor. Show that average power cousumed per cycle in an a.c. circuit conataining an ideal capacitor is zero.
View SolutionDerive an experssion for the average power in LCR circuit connected to a.c. supply. Hence define power factor. Show that average power cousumed per cycle in an a.c. circuit conataining an ideal capacitor is zero.
View Solution
Knowledge Check
The average power in LCR series circuit is
AermsIrmscosϕBermsIrmssinϕCermsIrmsDermsIrmstanϕ
Obtain anexpression for the average power of an a.c circuit .
View Solution(a) Deriver and expression for the average power consumed in a series LCR circuit connected to a.c., source in which the phase different between the voltage and the current in the circuit is ϕ.
(b) Define the quality factor in an a.c. circuit. Why should the quality factor have high value in receiving circuits ? Name the factors on which it depends.
View SolutionA voltage V=Vmsinωt is applied to a series L-C-R circuit. Derive the expression for the average power dissipated over a cycle. Under what condition (i) no power is dissipated even though the current flows through the circuit, (ii) maximum power is dissipated in the circuit ?
View SolutionA voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionA voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionThe average power in LCR series circuit is
View SolutionDerive the expression for the power dissipated by an ideal resistor in an AC circuit .
View Solution

