A tap is dripping at a constant rate into a container. The level (Lcm) of the water in the container is given by the equation L=2−2t , where t is time taken in hours. Then the level of water in the container at the start is
0 cm
1 cm
2 cm
4 cm
The correct Answer is:B
To find the level of water in the container at the start (when time t=0), we can use the given equation:
L=2−2t
1. Identify the time at the start:
- At the start, time t=0.
2. Substitute t=0 into the equation:
- We substitute t=0 into the equation L=2−2t:
L=2−20
3. Calculate 20:
- We know that any number raised to the power of 0 is 1:
20=1
4. Substitute back into the equation:
- Now substitute 20=1 back into the equation:
L=2−1
5. Perform the subtraction:
- Now, calculate 2−1:
L=1
6. Conclusion:
- Therefore, the level of water in the container at the start is 1 centimeter.
Final Answer:
The level of water in the container at the start is 1 centimeter.
- At the start, time t=0.
- We substitute t=0 into the equation L=2−2t:
L=2−20
- We know that any number raised to the power of 0 is 1:
20=1
- Now substitute 20=1 back into the equation:
L=2−1
- Now, calculate 2−1:
L=1
- Therefore, the level of water in the container at the start is 1 centimeter.
The level of water in the container at the start is 1 centimeter.
Topper's Solved these Questions
- POWER, INDICES AND SURDSBOOK - KIRAN PUBLICATIONCHAPTER - POWER, INDICES AND SURDSEXERCISE - Type -VI
17 Videos
- POWER, INDICES AND SURDSBOOK - KIRAN PUBLICATIONCHAPTER - POWER, INDICES AND SURDSEXERCISE - Type -VII
34 Videos
- POWER, INDICES AND SURDSBOOK - KIRAN PUBLICATIONCHAPTER - POWER, INDICES AND SURDSEXERCISE - Type -IV
198 Videos
- PIPE AND CISTERN BOOK - KIRAN PUBLICATIONCHAPTER - PIPE AND CISTERN EXERCISE - TIPE-IV
9 Videos
- PROFIT AND LOSS BOOK - KIRAN PUBLICATIONCHAPTER - PROFIT AND LOSS EXERCISE - TEST YOURSELF
23 Videos
Similar Questions
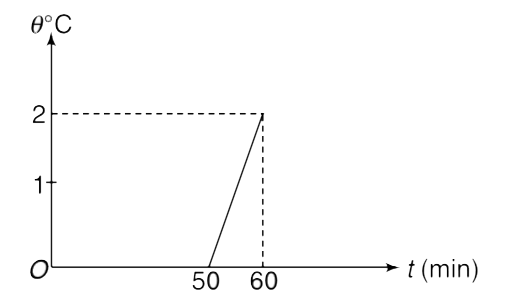
A container contains 5 kg of water at 0∘C mixed to an unknown mass of ice in thermal equilibrium. The water equivalent of the container is 100 g. At time t = 0, a heater is switched on which supplies heat at a constant rate to the container. The temperature of the mixture is measured at various times and the result has been plotted in the given figure. Neglect any heat loss from the mixture – container system to the surrounding and calculate the initial mass of the ice.
Given: Sp. latent heat of fusion of ice is Lf=80calg−1
Sp. heat capacity of water =1calg−1.∘C−1
View SolutionTwo open containers A and B are filled with water and in container A, cetyl alcohol is added. Both the containers are placed at 40∘C. Predict the level of water in the two containers after some time and give reasons.
View Solution
Knowledge Check
A tap is dripping at a constant rate into a container. The level (Lcm) of the water in the container is given by the equation L=2−2t , where t is time taken in hours. Then the level of water in the container at the start is
A0 cmB1 cmC2 cmD4 cmA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
A12pt31B13pt21C12pt21D12pt31An ice block contains a glass ball when the ice melts within the water containing vessel, the level of water
ARisesBFallsCUnchangedDFirst rises and then falls
Two open containers A and B are filled with water and in container A, cetyl alcohol is added. Both the containers are placed at 40∘C. Predict the level of water in the two containers after some time and give reasons.
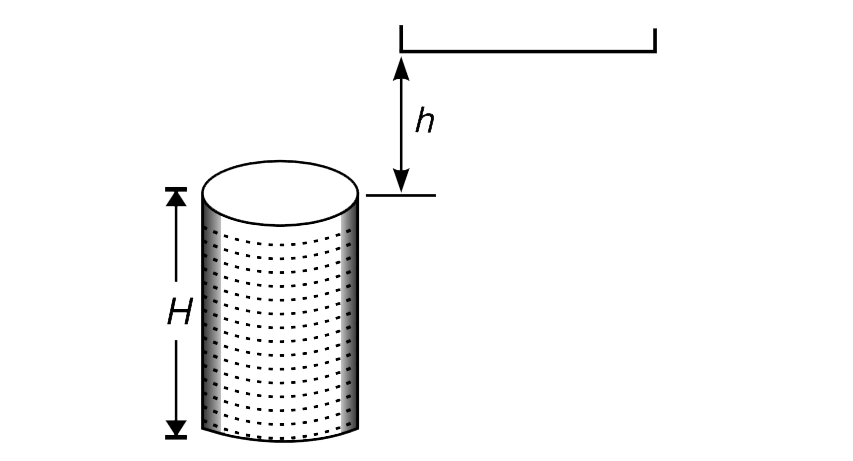
View SolutionA completely filled cylinderical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
View SolutionA container contains 35 kg water and 0.2 kg water leaks from the container. Find the amount of water in container.
View SolutionA container has 80 L of milk. From this container 8 L of milk was taken out and replaced by water. The process was further repeated twice. The volue of milk in the container after that is :
View SolutionA piece of ice is floating in a jar containing water. When the ice melts, then the level of water
View Solution
