There are some boys and girls in a room. The square of the number of the girls is less than the square of the number of boys by 28. If there were two more girls, the number of boys would have been the same as that of the girls. The total number of the boys and girls in the room are
56
14
10
7
The correct Answer is:B
To solve the problem step by step, we will define variables for the number of boys and girls and set up equations based on the information provided.
Step 1: Define Variables
Let:
- X = number of boys
- Y = number of girls
Step 2: Set Up the First Equation
According to the problem, the square of the number of girls is less than the square of the number of boys by 28. This can be expressed mathematically as:
X2−Y2=28
Step 3: Set Up the Second Equation
The problem also states that if there were two more girls, the number of boys would be equal to the number of girls. This can be expressed as:
X=Y+2
Alternatively, we can rearrange this to:
X−Y=2
Step 4: Substitute the Second Equation into the First
We can use the second equation X−Y=2 to express X in terms of Y:
X=Y+2
Now, substitute X into the first equation:
(Y+2)2−Y2=28
Step 5: Expand and Simplify
Expanding the left side:
(Y2+4Y+4)−Y2=28
This simplifies to:
4Y+4=28
Step 6: Solve for Y
Subtract 4 from both sides:
4Y=24
Now, divide by 4:
Y=6
Step 7: Find X
Now that we have Y, we can find X using the equation X=Y+2:
X=6+2=8
Step 8: Calculate the Total Number of Boys and Girls
Now, we can find the total number of boys and girls:
X+Y=8+6=14
Final Answer
The total number of boys and girls in the room is:
14
Let:
- X = number of boys
- Y = number of girls
According to the problem, the square of the number of girls is less than the square of the number of boys by 28. This can be expressed mathematically as:
X2−Y2=28
The problem also states that if there were two more girls, the number of boys would be equal to the number of girls. This can be expressed as:
X=Y+2
Alternatively, we can rearrange this to:
X−Y=2
We can use the second equation X−Y=2 to express X in terms of Y:
X=Y+2
(Y+2)2−Y2=28
Expanding the left side:
(Y2+4Y+4)−Y2=28
This simplifies to:
4Y+4=28
Subtract 4 from both sides:
4Y=24
Now, divide by 4:
Y=6
Now that we have Y, we can find X using the equation X=Y+2:
X=6+2=8
Now, we can find the total number of boys and girls:
X+Y=8+6=14
The total number of boys and girls in the room is:
14
Topper's Solved these Questions
- SIMPLIFICATIONBook:KIRAN PUBLICATIONChapter:SIMPLIFICATIONExercise:TYPE-II
Explore 43 Videos
- SIMPLIFICATIONBook:KIRAN PUBLICATIONChapter:SIMPLIFICATIONExercise:TYPE-III
Explore 17 Videos
- SIMPLE INTERSETBook:KIRAN PUBLICATIONChapter:SIMPLE INTERSETExercise:TEST YOURSELF
Explore 25 Videos
- STATISTICS AND DATA INTERPRETATIONBook:KIRAN PUBLICATIONChapter:STATISTICS AND DATA INTERPRETATIONExercise:TYPE-VIII
Explore 8 Videos
Similar Questions
There are some boys and girls in a room. The square of the number of girls is less than the square of the number of boys by 28. If there were two more girls, the number of boys would have been the same as that of the girls. The total number of boys and girls in the room is (a) 7 (b) 10 (c) 14 (d) 56
View SolutionThere are 30 boys and 20 girls in a class. The ratio of the number of girls to the number of boys is
View Solution
Knowledge Check
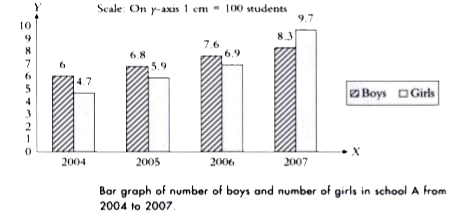
In which year the number of girls is more than the number of boys?A2004B2005C2006D2007There are 1550 boys and girls in a school. The number of girls exceeds the number of boys by 500. What is the percentage (to nearest integer) of girls in the school?
A67%B66%C64%D65%There are 1550 boys and girls in a school. The number of girls exceeds the number of boys by 500. What is the percentage (to nearest integer) of girls in the school ?
Aa) 67%Bb) 66%Cc) 64%Dd) 65%
The number of boys and girls in a class are in the ratio 5:4. If the number of boys is 9 more than the number of girls, then number of boys is 9.
View SolutionIn a class, if 60% of the students are boys and the number of girls is 36, then the number of boys is:
View SolutionIn a class, the no. of boys is more than the no. of girls by 12% of the total strength. The ratio of boys to girls is :
View SolutionThe number of boys in a class is 2/5 of the number of girls. If the number of boys in the class is 10, find the number of girls.
View SolutionThe number of boys is more than the number of girls by 12% of the total strength of the class. The ratio of the number of boys to that of the girls is
View Solution
