Three independent events. A1,A2 and A3 occur with probabilities P(Ai)=11+i,i=1,2,3. What is the probability that at least one of the three events occurs?
14
23
34
124
The correct Answer is:C
To find the probability that at least one of the three independent events A1,A2, and A3 occurs, we can follow these steps:
Step 1: Determine the probabilities of each event
Given the probabilities:
- P(A1)=11+1=12
- P(A2)=11+2=13
- P(A3)=11+3=14
Step 2: Calculate the probabilities of the complements of each event
The complements of the events are:
- P(A′1)=1−P(A1)=1−12=12
- P(A′2)=1−P(A2)=1−13=23
- P(A′3)=1−P(A3)=1−14=34
Step 3: Calculate the probability that none of the events occur
Since the events are independent, the probability that none of the events occur is given by:
P(A′1∩A′2∩A′3)=P(A′1)×P(A′2)×P(A′3)
Calculating this:
P(A′1∩A′2∩A′3)=12×23×34
=1×2×32×3×4=624=14
Step 4: Calculate the probability that at least one event occurs
The probability that at least one of the events occurs is:
P(A1∪A2∪A3)=1−P(A′1∩A′2∩A′3)
Substituting the value we found:
P(A1∪A2∪A3)=1−14=34
Final Answer
Thus, the probability that at least one of the three events occurs is 34.
---
Given the probabilities:
- P(A1)=11+1=12
- P(A2)=11+2=13
- P(A3)=11+3=14
The complements of the events are:
- P(A′1)=1−P(A1)=1−12=12
- P(A′2)=1−P(A2)=1−13=23
- P(A′3)=1−P(A3)=1−14=34
Since the events are independent, the probability that none of the events occur is given by:
P(A′1∩A′2∩A′3)=P(A′1)×P(A′2)×P(A′3)
Calculating this:
P(A′1∩A′2∩A′3)=12×23×34
=1×2×32×3×4=624=14
The probability that at least one of the events occurs is:
P(A1∪A2∪A3)=1−P(A′1∩A′2∩A′3)
Substituting the value we found:
P(A1∪A2∪A3)=1−14=34
Thus, the probability that at least one of the three events occurs is 34.
Topper's Solved these Questions
- PROBABILITYBOOK - PUNEET DOGRACHAPTER - PROBABILITYEXERCISE - PREV YEAR QUESTIONS
159 Videos
- POINT & LINE BOOK - PUNEET DOGRACHAPTER - POINT & LINE EXERCISE - PREV YEAR QUESTIONS
105 Videos
- PROPERTIES OF TRIANGLES BOOK - PUNEET DOGRACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - PREV YEAR QUESTION
30 Videos
Similar Questions
Knowledge Check
Three independent events. A1,A2 and A3 occur with probabilities P(Ai)=11+i,i=1,2,3. What is the probability that at least one of the three events occurs?
A14B23C34D124If A1,A2,A3....,A8 are independent events such that P(Ai)=11+i where 1≤I≤8, then probability that none of them will occur is
A29B13C12D19An observed event B can occure after one of the three events A1,A2,A3. If P(A1)=PA2=0.4,P(A3)=0.2 and P(B/A1)=0.25,P(B/A2)=0.4,P(B/A3)=0.125 what is the probability of A1 after observing B ?
AA. 13BB. 619CC. 2057DD. 25
If A1,A2,A3,........A1006 be independent events such that P(A)=12i(i=1,2,3,.....1006) and probability that none of the events occur be α!2α(β!)2. then
View Solution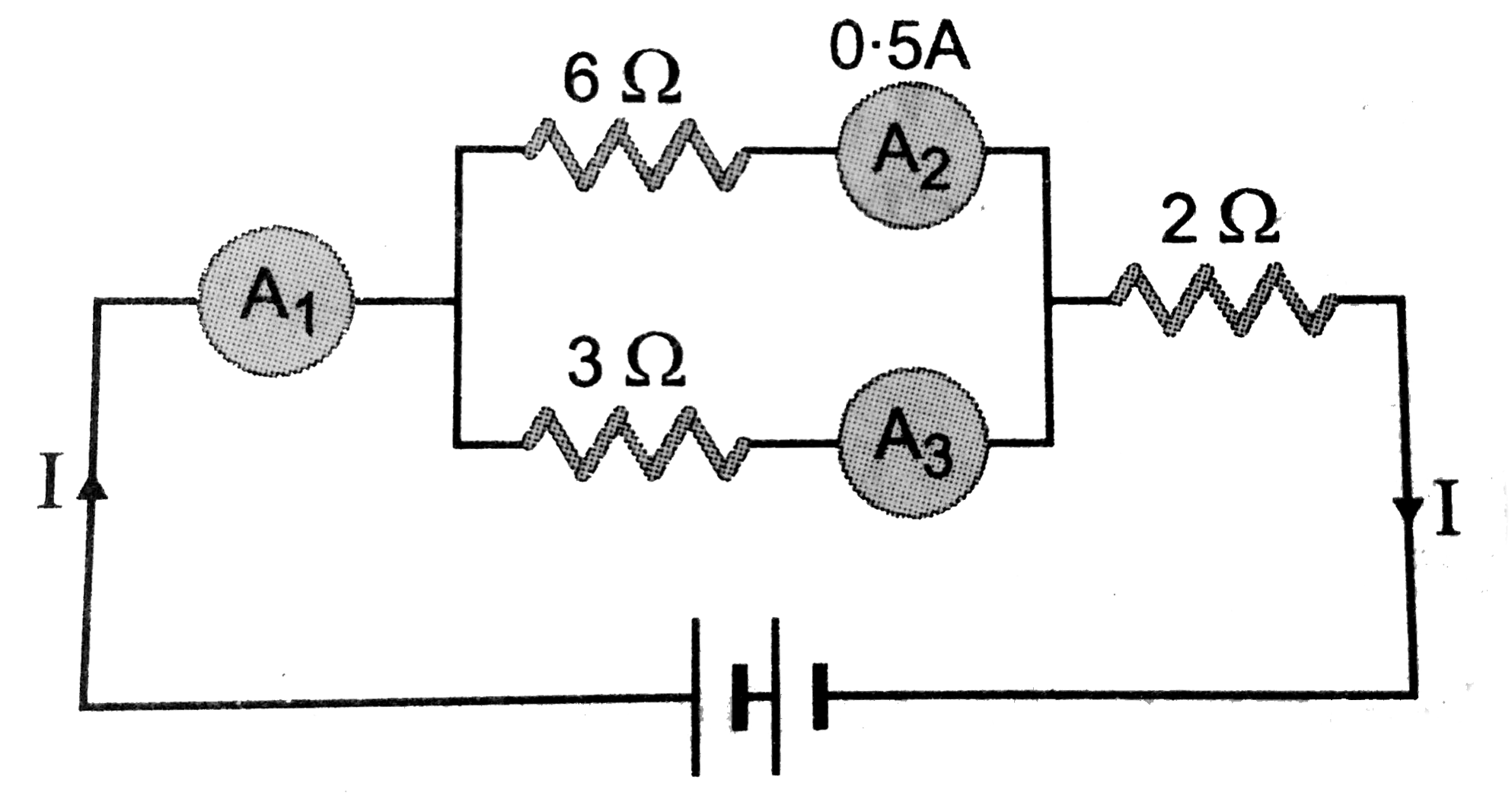
A1,A2andA3 Are the ammeters and A2 reads 0.5A. (i) What are the readings of ammeters A1 and A3 ? (ii) What is the total resistance of the circuit ?
View SolutionAn observed event B can occur after one of the three events A1,A2,A3. If
P(A1)=P(A2)=0.4,P(A3)=0.2andP(B/A1)=0.25,P(B/A2)=0.4,P(B/A3)=0.125, what is the probability of A1 after observing B ?
View SolutionIf A1,A2,..,An are any n events, then
View SolutionLet points A1,A2andA3 lie on the parabola y2=8x. If △A1A2A3 is an equilateral triangle and normals at points A1,A2andA3 on this parabola meet at the point (h, 0). Then the value of h I s
View Solution
