What is the number of different messages that can be represented by three 0's and two 1's ?
10
9
8
7
The correct Answer is:A
To find the number of different messages that can be represented by three 0's and two 1's, we can use the concept of permutations of multiset. Here are the steps to solve the problem:
Step 1: Identify the total number of symbols
We have a total of 5 symbols: three 0's and two 1's.
Step 2: Use the formula for permutations of multiset
The formula to find the number of distinct arrangements of n items where there are groups of identical items is given by:
Number of arrangements=n!n1!×n2!
Where:
- n is the total number of items,
- n1 is the number of identical items of one type (0's),
- n2 is the number of identical items of another type (1's).
Step 3: Substitute the values into the formula
In our case:
- n=5 (total symbols),
- n1=3 (for the three 0's),
- n2=2 (for the two 1's).
So, we can substitute these values into the formula:
Number of arrangements=5!3!×2!
Step 4: Calculate the factorials
Now, we calculate the factorials:
- 5!=5×4×3×2×1=120
- 3!=3×2×1=6
- 2!=2×1=2
Step 5: Substitute the factorial values back into the equation
Now we substitute these values back into the equation:
Number of arrangements=1206×2=12012=10
Step 6: Conclusion
Thus, the number of different messages that can be represented by three 0's and two 1's is 10.
We have a total of 5 symbols: three 0's and two 1's.
The formula to find the number of distinct arrangements of n items where there are groups of identical items is given by:
- n is the total number of items,
- n1 is the number of identical items of one type (0's),
- n2 is the number of identical items of another type (1's).
In our case:
- n=5 (total symbols),
- n1=3 (for the three 0's),
- n2=2 (for the two 1's).
Now, we calculate the factorials:
- 5!=5×4×3×2×1=120
- 3!=3×2×1=6
- 2!=2×1=2
Now we substitute these values back into the equation:
Thus, the number of different messages that can be represented by three 0's and two 1's is 10.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A byte can represent any number between 0 and
A2B255C256D10248 more than three times the number x can be represented as
A8+x+3B3x−8C3x+8D8x+3In two different system of unit an acceleration is represented by the same number, whilst a velocity is represented by numbers in the ratio 1:3. The ratio of unit of length and time are
A13,19B19,13C1,1DNone of these
What is the maximum number of orbital(s) that can be associated with the following quantum numbers? (n=4,l=1,m1=0)
View SolutionWhat is the oxidation number of S in S8.
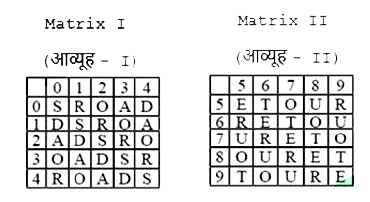
View SolutionIn the following question, a word is represented by only one set of numbers as given in any one of the alternatives. The set of numbers given in the alternatives is represented by two classes of alphabets as in two matrices given below. The columns and rows of Matrix I and Matrix II are numbered as given. A letter from these matrices can be represented first by its row and next by its column, example, R can be represented by 65, 76 and S can be represented by 11, 22, etc.
Identity the set for the word DEAR.
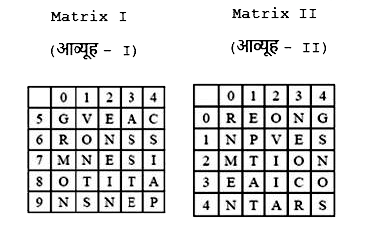
View SolutionIn the following question, a word is represented by only one set of numbers as given in any one of the alternatives. The set of numbers given in the alternatives is represented by two classes of alphabets as in two matrices given below. The columns and rows of Matrix I and Matrix II are numbered as given. A letter from these matrices can be represented first by its row and next by its column, example, R can be represented by 60, 43 and S can be represented by 73, 44, etc.
Identify the set for the word RAIN.
View SolutionIn the following question, a word is represented by only one set of numbers as given in any one of the alternatives. The set of numbers given in the alternatives is represented by two classes of alphabet as in two matrices given below. The columns and rows of Matrix I are numbered 0 to 4 and that of Matrix II are numbered 5 to 9. A letter from these matrices can be represented first by its row and then by its column, for example, 'S' can be represented by 14, 23, etc. and 'E' can be represented by 56, 68, etc. CURE

View Solution
