If the graph a quadratic polynomial lies entirely above x-axis. Which one of the following is correct ?
Both the roots are real
One root is real and the other is complex
Both the roots are complex
Can not say
The correct Answer is:C
To solve the question, we need to analyze the properties of the graph of a quadratic polynomial and its roots when the graph lies entirely above the x-axis.
1. Understanding the Quadratic Polynomial:
A quadratic polynomial can be expressed in the standard form as:
f(x)=Ax2+Bx+C
where A, B, and C are constants and A≠0.
2. Graph Behavior:
If the graph of this quadratic polynomial lies entirely above the x-axis, it means that for all values of x, f(x)>0. This indicates that there are no points where the graph intersects or touches the x-axis.
3. Roots of the Quadratic:
The roots of the quadratic equation Ax2+Bx+C=0 can be determined using the discriminant D:
D=B2−4AC
The nature of the roots is determined by the value of D:
- If D>0, there are two distinct real roots.
- If D=0, there is one real root (a repeated root).
- If D<0, there are two complex roots.
4. Condition for Entirely Above the x-axis:
Since the graph lies entirely above the x-axis, it cannot have any real roots (as real roots would imply the graph touches or crosses the x-axis). Therefore, the discriminant must be less than zero:
D<0⟹B2−4AC<0
This indicates that the quadratic has two complex roots.
5. Conclusion:
Based on the analysis, the correct statement is that both roots are complex. Therefore, the answer is:
Option C: Both the roots are complex.
A quadratic polynomial can be expressed in the standard form as:
f(x)=Ax2+Bx+C
where A, B, and C are constants and A≠0.
If the graph of this quadratic polynomial lies entirely above the x-axis, it means that for all values of x, f(x)>0. This indicates that there are no points where the graph intersects or touches the x-axis.
The roots of the quadratic equation Ax2+Bx+C=0 can be determined using the discriminant D:
D=B2−4AC
The nature of the roots is determined by the value of D:
- If D>0, there are two distinct real roots.
- If D=0, there is one real root (a repeated root).
- If D<0, there are two complex roots.
Since the graph lies entirely above the x-axis, it cannot have any real roots (as real roots would imply the graph touches or crosses the x-axis). Therefore, the discriminant must be less than zero:
D<0⟹B2−4AC<0
This indicates that the quadratic has two complex roots.
Based on the analysis, the correct statement is that both roots are complex. Therefore, the answer is:
Option C: Both the roots are complex.
Topper's Solved these Questions
- QUADRATIC EQUATIONSBook:PUNEET DOGRAChapter:QUADRATIC EQUATIONSExercise:PREV YEAR QUESTIONS
Explore 103 Videos
- PROPERTIES OF TRIANGLES Book:PUNEET DOGRAChapter:PROPERTIES OF TRIANGLES Exercise:PREV YEAR QUESTION
Explore 30 Videos
- SEQUENCE AND SERIESBook:PUNEET DOGRAChapter:SEQUENCE AND SERIESExercise:PREVIOUS YEAR QUESTIONS
Explore 88 Videos
Similar Questions
Knowledge Check
2x2+3x−α−0 has roots −2andβ while the equation x2−3mx+2m2=0 has both roots positive, where α>0andβ>0.
If the graph of a quadratic polynomial lies entirely above x-axis, then which one of the following is correct ?ABoth the roots are realBOne root is real and the other is complexCBoth the roots are complexDCannot sayThe graph of a quadratic equation is symmetrical about X-axis, which ones of the following can't be the roots of a quadratic equation?
AA)(0,0)BB)(−23,23)CC)(2√3,−2√3)DD)(4+√2,4−√2)The graph of a quadratic polynomial y=ax2+bx+c,a,b,c∈R is as shown.
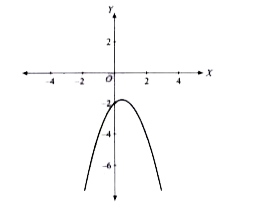
Which one of the is NOT correct ?Ab2−4ac<0Bca<0Cc is negativeDabscissa corresponding to the vertex is (−b2a)
Consider the graph of quadratic polynomial y=ax2+bx+c as shown below. Which of the following is/are correct?
View SolutionIf both the roots of a quadratic equation are coincident, which one of the following is not correct?
View SolutionGraph of Quadratic Polynomial(how to draw)
View SolutionIf one root of a quadratic equation is zero, which one of the following is correct?
View SolutionGraph of quadratic polynomial When polynomial have no zeroes
View Solution