m द्रव्यमान व r त्रिज्या का एक गोला एक क्षैतिज सतह पर इस प्रकार धकेला जाता है कि यह प्रारम्भ से बिना फिसले लुढक सके। तली पर द्रव्यमान केन्द्र की न्यूनतम चाल ज्ञात कीजिये ताकि यह (R+r) त्रिज्या के लूप के चारो ओर पूर्णतया लुढ़क सके। (बिना पथ को मुक्त किए)
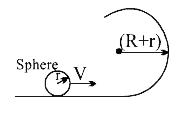
A बिन्दु पर कुल ऊर्जा
EA=EK+EP=mgh...(i)
B बिन्दु की ऊंचाई = 27 जहाँ । = पाश-पथ की त्रिज्या है । - अगर B बिन्दु पर गेंद का न्यूनतम वेग v हो, तो
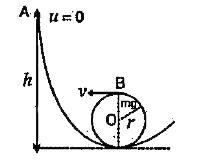
mv2r=mg,∴v2=rg
∴ B बिन्दु पर कुल ऊर्जा,
EB=EK+EP=12mv2+mg(2r)
=12mrg+2mgr=52mgr
ऊर्जा-संरक्षण सिद्धान्त से,
EA=EB
mgh=52mgr,∴h=5r2
Topper's Solved these Questions
- गति के नियम BOOK - STUDENTS FRIENDSCHAPTER - गति के नियम EXERCISE - अभ्यासार्थ प्रश्नमाला (वस्तुनिष्ठ प्रश्न)
35 Videos
- गति के नियम BOOK - STUDENTS FRIENDSCHAPTER - गति के नियम EXERCISE - अभ्यासार्थ प्रश्नमाला (रिक्त स्थानों को भरे)
8 Videos
- कार्य ऊर्जा और शक्तिBOOK - STUDENTS FRIENDSCHAPTER - कार्य ऊर्जा और शक्तिEXERCISE - सैद्धान्तिक प्रश्नोत्तर
3 Videos
- गतिकीBOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((E) आंकिक:)
5 Videos
Similar Questions
वृत्तीय पथ पर चलनेवाली वस्तु में
View Solutionन्यूटन की गति के किस नियम से बल की परिभाषा मिलती है ?
View Solutionएक कार और एक लॉरी, (Lorry) समान गतिज ऊर्जा से गतिशील है । अगर उन पर समान अवरोधी बल (Breaking force) आरोपित किया जाये तो क्या रुकते-रुकते समान दूरी तय करेंगे?
View Solutionअगर →a=→3i−4→j और →b=→8i+→6j तब →a,→b,→a+→b,→a−→b ओर →b−→a का मापांक और दिशा निकालें ।
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solutionमंथन के पश्चात दूध को कपड़े के एक टुकड़े पर उढ़ेलने पर क्रीम उस पर रह जाता है। पृथक्करण की यह प्रक्रिया ...... कहलाती है।
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solution
