Prove that distance travelled by a body in the nth second is Sn=u+a2(2n−1) Solution in Punjabi
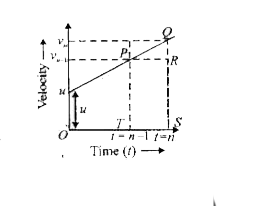
The v-t graph for uniformaly acceerated motion is as shown in the Let vn−1andvn be the velocities at t = n -1 and t = n.
Distance travelled by the particle in nth second = area of treapezium PQST=12(PT+QS)×TS
or Snth=12(vn−1+vn)×[n−(n−1)]
=12(vn−1+vn) ...(i)
We know that, v=u+at
∴vn−1=u+a(n−1)andvn=u+an
Substituting value of vn−1andvn in (i) we get
Snth=12[u+a(n−1)+u+an]
=12(2u)+12(2an−a)
orSnth=u+a2(2n−1)
Similar Questions
The distance travelled by a particle in nth second is Sn=u+a2(2n−1) where u is the velocity and a is the acceleration. The equation is
View SolutionA freely falling body traveled xm in nth second distance travelled in n−1th second is
View SolutionA body starts from rest and its distance covered in n" second is given by Snth=a2(2n−1) ,when 'a' is acceleration of the body. Then SI unit of Snth is
View SolutionUse integeration technique to prove that the distance travelled in nth second: snth=u+a2(2n−1)
View SolutionA freely falling body traveled xm in nth second distance travelled in n−1th second is
View SolutionA freely falling body traveled xm in nth second distance travelled in n−1th second is
View SolutionThe distance travelled by a particle in n^(th) second is S_(n) = u + (a)/(2) (2n-1) where u is the velocity and a is the acceleration. The equation is
View SolutionWith usual notation, the following equation, said to give the distance covered in the nth second. i.e.,<br>S_(n)=u+(a2n−12) is
View Solution
