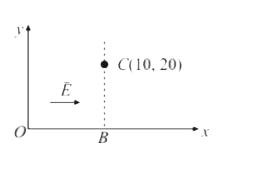
An electric field $\to E = ˆ i$ Cx exists in the space, where C = 10 V/ $m^{2}$ . Taking the potential at (10 m, 20 m ) to be zero, find the potential at the origin.

A

1000 V

B

500 V

C

250 V

D

100 V

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Figure shows the situation described in question. Here BC is the equipotential line so we can use $V_{C} = V_{B} = 0$
If $V_{0}$ be the potential at the origin, we can use
$V_{0} - V_{B} = \int_{0}^{B} E d x = \int_{0}^{10} A x d x$
$\Rightarrow V_{0} - 0 = A {∣ ∣ ∣ \frac{x^{2}}{2} ∣ ∣ ∣}_{0}^{10} = 10 \times \frac{10^{2}}{2} \Rightarrow V_{0} = 500 V$

|

Updated on:21/07/2023

Class 12 PHYSICS QUIZ

Similar Questions

Knowledge Check

Question 1 - Select One
Assume that an electric field $\to E = 30 x^{2} ˆ i$ exists in space. Then the potentail differences $V_{A} - V_{0}$ where $V_{0}$ is the potential at the origin and $V_{A}$ , the potebntail at $x = 2 m$ is
A $- 80 V$
B $80 V$
C $120 V$
D $- 120 V$
Question 2 - Select One
An electric field $E = (20 ˆ i + 30 ˆ j)$ N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at $(2 m, 2 m)$ .
A $- 100 V$
B $- 200 V$
C $- 300 V$
D $- 400 V$
Question 3 - Select One
An electric field $\to E = 20 y ˆ j$ exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
A500 V
B250 V
C125 V
DZero

Recommended Questions

Home
Ask Doubt
Profile