1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
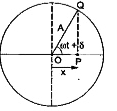
चित्र 4.11 में एक कण को अचर कोणीय चाल ω से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति ωt+δ हैं यहाँ δ इस कण की t=0 पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
x=Acos(ωt=δ)
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
x=(4.0m)cos{(4π rad s−1)t+π3 rad}
तो
1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है। चित्र 4.11 में एक कण को अचर कोणीय चाल omega से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति omegat+delta हैं यहाँ delta इस कण की t=0 पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है। x=Acos(omegat=delta) जो कि सरल आवर्त गति का समीकरण है यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है, x=(4.0m)cos{(4pi
सरल आवर्त गति का दोलन - काल या एकसमान वृत्तीय गति का परिक्रमण काल है

A

4.0 s

B

2.0 s

C

1.0 s

D

0.5 s

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for 1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है। चित्र 4.11 में एक कण को अचर कोणीय चाल omega से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति omegat+delta हैं यहाँ delta इस कण की t=0 पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है। x=Acos(omegat=delta) जो कि सरल आवर्त गति का समीकरण है यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है, x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"} तो सरल आवर्त गति का दोलन - काल या एकसमान वृत्तीय गति का परिक्रमण काल है by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions