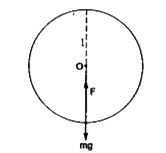
एक मीटर अतानित (unstretched) लंबाई के इस्पात के तार के एक सिरे से 4 kg का द्रव्यमान बाँधकर उसे एक ऊर्ध्वाधर वृत्त (vertical circle) में घुमाया जाता है (चित्र1.10-5 ) , वृत्त के निम्नतम बिंदु पर उसका कोणीय वेग 120 rpm है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 5.6(mm)2 है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिंदु (lowest point) पर है (g=10ms−2 और इस्पात के लिए Y=2×1011Nm−2)
दिया गया है कि
l = 1 m
m = 4 kg
ω=12r±=120×2π60rads−1=4πrads−1
A=5.6mm2=5.6×10−6m2
g=10ms−2
ऊर्ध्वाधर वृत्त के निम्नतम बिंदु पर तार द्वारा द्रव्यमान का कुल परिणामी बल
F=mg+mω2l या F=m(g+ω2l)
=(4kg)(10+(4π)2×1)ms−2
=4[10+16×(3.142)2]N
=671N
सूत्र Y=(F/A)(Δl/l) से
Δl=FlAY=671N×1m5.6×10−6m2×2×1011Nm−2
=6×10−4m=0.60mm
अतः वृत्त के निम्नतम बिंदु पर तार में विस्तार 0 . 60 m m है।
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.11 लघु दोलन : सरल आवर्त गति : लोलक
31 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव
19 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1. 9 गुरुत्वाकर्षण
25 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
x-अक्ष पर गतिशील कण के लिए चार स्थिति - समय ग्राफ (x-t graph) चित्र 1.11-1 में प्रदर्शित है। कारण स्पष्ट करते हुए बताएँ कि इनमे कौन- कौन से ग्राफ द्वारा आवर्ती गति (periodic motion) व्यक्त होती है तथा उनके आवर्तकाल क्या है ?

View Solutionदो पात्रों (vessels) के आधारों के क्षेत्रफल समान है , परंतु आकृतियाँ (shapes) भिन्न - भिन्न है। पहले पात्र के दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है क्या दोनों प्रकरणो (cases) के पात्रो के आधारों पर आरोपित बल समान है ?
View Solutionकिसी विघुत आवेश को अन्य आवेशों के वैघुत बलों से परिरक्षित (shield ) करने के लिए उस आवेश को खोखले चालक के अंदर रखा जाता है । क्या किसी वस्तु को अन्य द्रव्यमान के गुरुत्वीय बलों से परिरक्षित करने के लिए उसे किसी खोखले गोले में रखकर या किसी अन्य साधन द्वारा ऐसा किया जा सकता है ?
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
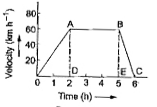
View Solution10 g द्रव्यमान और 50 m/s चाल वाली बंदूक की गोली एक दरवाजे में अंतः स्थापित हो जाती है । दरवाजा 1.0 M चौड़ा है और इसका द्रव्यमान 12 kg है इसके एक सिरे पर कब्जे लगे है और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए ।
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionकिसी वृत्त के जीवा का मध्य बिंदु दिया है
View SolutionA solid sphere of brass with a radius 15 cm is drawn into a wire of diameter 6 mm. The length of the wire ( in cm ) is :
15 cm त्रिज्या वाले पीतल के एक ठोस गोले को 6 mm व्यास के तार में खिंचा जाता है | तार की लम्बाई (cm में) है:
View SolutionIf 3.96 cubic dm of lead is to be drawn in to a cylindrical wire of diameter 0.6 cm, then the length of the wire (in metres), is: यदि सीसा 3.96 घन डेसीमीटर है जिससे एक 0.6 सेमी व्यास के बेलनाकार तार को बनाना है, तो तार की लंबाई (मीटर में) है:
View SolutionA chord 10 cm long is drawn in a circle of diameter 26 cm. The perpendicular distance of the chord from the centre is: एक तार 10 सेमी लंबी, व्यास 26 सेमी के एक वृत्त में खींचा जाता है। केंद्र से जीवा की लंबवत दूरी है
View Solutionवृत्त के एक बिंदु पर स्पर्श रेखा का समीकरण#!#उदाहरण
View Solutionएक बिंदु पर वृत्त के अभिलम्ब का समीकरण#!#उदाहरण
View Solution
