प्रक्षेप के पथ का समीकरण प्राप्त करें।
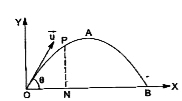
मान लिया कि प्रक्षेप बिंदु O है जिसे मूलबिंदु (origin) माना गया है। मान लिया कि प्रक्षेप पथ OPAB है जिसके किसी बिंदु P के नियामक (coordinates), OX तथा OY अक्षों के सापेक्ष x तथा y हैं। अतः, ON = x तथा PN = y. चित्र में OX तथा OY दिशाएँ क्रमशः क्षैतिज तथा ऊध्र्वाधर दिशाएँ व्यक्त करती हैं। मान लिया कि किसी वस्तु को क्षतिज तल से एकोण पर वेग से फेंका जाता है और मान लिया कि वस्तु ! समय के बाद बिंदु P(x, y) पर पहुँचती है तो वेग →u का क्षैतिज घटक ux=ucosθ तथा ऊधिर घटक uy=usinθ अतः, क्षैतिज दिशा OX में गति के लिए
ON=x=uxt=ucosθ×t⇒t=xucosθ
तथा ऊर्ध्वाधर दिशा में OY में गति के लिए
NP=y=uyt−12gt2=usinθ×xucosθ−12g((x)(ucosθ))2
y=(tanθ)x−(g2u2cos2θ)x2
उपर्युक्त समीकरण का रूप y=ax−bx2 जैसा है जो मूलबिंदु से होकर जानेवाले परवलय (parabola) के समीकरण को व्यक्त करता है। अतः, स्पष्ट है कि समीकरण (1) द्वारा व्यक्त प्रक्षेप (projectile) का प्रक्षेप पथ (path of projectile) परवलयिक (parabolic) होता है।
Topper's Solved these Questions
- सरल रेखा एवं समतल, में कण की गति Book:DAS GUPTAChapter:सरल रेखा एवं समतल, में कण की गति Exercise: प्रश्नावली (दीर्घ उत्तरीय प्रश्न )
Explore 2 Videos
- सरल रेखा एवं समतल, में कण की गति Book:DAS GUPTAChapter:सरल रेखा एवं समतल, में कण की गति Exercise: प्रश्नावली (आंकिक प्रश्न)
Explore 24 Videos
- सरल रेखा एवं समतल, में कण की गति Book:DAS GUPTAChapter:सरल रेखा एवं समतल, में कण की गति Exercise: प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
Explore 13 Videos
- वित्तीय गत्तिBook:DAS GUPTAChapter:वित्तीय गत्तिExercise:प्रश्नावली ( आंकिक प्रश्न )
Explore 12 Videos
- सामान्य भौतिकीBook:DAS GUPTAChapter:सामान्य भौतिकीExercise:1 . 13 बरनूली - प्रमेय : श्यानता
Explore 15 Videos
Similar Questions
प्रक्षेप्य गति क्या है? प्रक्षेप्य गति के लिए महत्तम ऊँचाई के लिए व्यंजक प्राप्त करें।
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
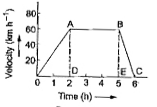
View Solutionविस्थापन कैसी राशि है-अदिश या सदिश?
View Solutionएक डोरी अधिक-से-अधिक 100 N का बल बिना टूटे सँभाल सकती है। इस डोरी के 1 m लंबे टुकड़े के एक सिरे पर 1kg द्रव्यमान की वस्तु को बाँधकर क्षैतिज तल में घुमाया जाता है। बताएँ कि बिना टूटे डोरी को वस्तुसहित किस अधिकत्तम चाल से घुमाया जा सकता है?
View Solutionजब हम किसी जल - टोटी (water tap) को अपनी उँगलियों द्वारा बंद करने का प्रयास करते है , तो उँगलियों के बीच की खली जगह से तीव्र जल - धाराएँ फुट निकलती है। व्याख्या करे।
View Solutionरासायनिक समीकरण से प्राप्त होने वाली सूचनाएँ || रासायनिक समीकरण के उपयोग से लाभ || रासायनिक समीकरण की सीमाएँ ||
View Solutionयदिa=2i−3j+6k और b=−2i+2j−k तब a का b पर प्रक्षेप (Projection)b का a पर प्रक्षेप (Projection) का मान होगा
View Solutionयदिa=2i−3j+6k और b=−2i+2j−k तब (a का b पर प्रक्षेप)/(b का a पर प्रक्षेप)का मान होगा
View Solutionसमतल के समीकरण का अंतः खंड-रूप
View Solutionसरल रेखाओ के समीकरण का लंब रूप
View SolutionX अक्ष का समीकरण |Y अक्ष का समीकरण |अक्षों के समांतर रेखाओ के समीकरण |NCERT प्रश्न |सारांश
View Solutionगति के समीकरण गणितीय विधि से #!#गति का द्वितीय समीकरण
View Solutionसदिश का प्रक्षेप [Projection]
View Solutionह्रदय का संवहन पथ | ह्रदय धड़कन का विनियमन के तंत्रिकीय विनियमन के प्रकार | हार्मोनल नियंत्रण
View Solutionप्रक्षेप्य पथ का समीकरण
View Solutionसमान परास के दो प्रक्षेप्यो की तुलना |प्रक्षेप पथ का समीकरण|प्रक्षेपण पर महत्वपूर्ण उदाहरण|OMR|Summary
View Solution

