A bird is at a height 60m from the surface of water and a fish is at a depth 40 m from surface. Both are at the same vertical line. What is the distance between them as seen by
Fish
To find the distance between the bird and the fish as seen by the fish, we can follow these steps:
Step 1: Understand the positions of the bird and the fish
- The bird is at a height of 60 meters above the surface of the water.
- The fish is at a depth of 40 meters below the surface of the water.
- Both are aligned vertically.
Step 2: Calculate the actual distance between the bird and the fish
- The actual distance (D_actual) between the bird and the fish can be calculated as:
Dactual=Height of the bird+Depth of the fish
Dactual=60m+40m=100m
Step 3: Determine the apparent height of the bird as seen by the fish
- Since the fish is in water (denser medium) and the bird is in air (rarer medium), we need to calculate the apparent height of the bird using the refractive index of water.
- The refractive index (n) of water is given as 43.
- The apparent height of the bird (H_B') can be calculated using the formula:
H′B=HBn
where HB is the actual height of the bird.
H′B=60m43=60m×34=45m
Step 4: Calculate the total distance as seen by the fish
- The total distance (D) between the fish and the apparent position of the bird as seen by the fish is:
D=Depth of the fish+Apparent height of the bird
D=40m+45m=85m
Final Answer
Thus, the distance between the bird and the fish as seen by the fish is 85 meters.
---
- The bird is at a height of 60 meters above the surface of the water.
- The fish is at a depth of 40 meters below the surface of the water.
- Both are aligned vertically.
- The actual distance (D_actual) between the bird and the fish can be calculated as:
Dactual=Height of the bird+Depth of the fish
Dactual=60m+40m=100m
- Since the fish is in water (denser medium) and the bird is in air (rarer medium), we need to calculate the apparent height of the bird using the refractive index of water.
- The refractive index (n) of water is given as 43.
- The apparent height of the bird (H_B') can be calculated using the formula:
H′B=HBn
where HB is the actual height of the bird.
H′B=60m43=60m×34=45m
- The total distance (D) between the fish and the apparent position of the bird as seen by the fish is:
D=Depth of the fish+Apparent height of the bird
D=40m+45m=85m
Thus, the distance between the bird and the fish as seen by the fish is 85 meters.
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - OLYMPIAD AND NSE LEVEL EXCERCISES
10 Videos
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - GENERAL EXERCISE
32 Videos
- OPTICAL INSTRUMENTS BOOK - CENGAGE PHYSICSCHAPTER - OPTICAL INSTRUMENTS EXERCISE - OLYMPLAD AND NTSE LEVEL EXERCISES
10 Videos
- SOURCES OF ELECTRIC CURRENTBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF ELECTRIC CURRENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
A bird in air is at a height ‘y’ from the surface of water. A fish is at a depth ‘x’ below the surface of water. The apparent distance of fish from the bird is (The refractive index of water is n )
Ax+yμBμx+yCxμ+yDxμ−yAcceleration due to gravity as same at height h from surface and at depth h from surface, then find value of h
A(5√−1)R2B(root5)R2−1CRroot2D(root5)R+r2A bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
A2.25mB3.33mC4mD4/3m
A plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
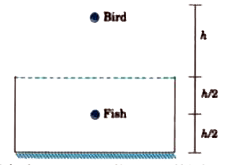
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
View SolutionAt what depth is the value of 'g' same as at a height of 40 km from the surface of earth.
View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionA bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View Solution
