A step index fibre has a relative refractive index difference of 0.9%.Estimate the critical angle at the core -cladding interface,when the core index is 1.46.find the numerical aperture,if the source to fiber medium is air.
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Understand the Given Information
- Relative refractive index difference (Δ) = 0.9% = 0.009 (as a decimal)
- Core refractive index (μ1) = 1.46
- We need to find the cladding refractive index (μ2) and the critical angle (θc) at the core-cladding interface.
Step 2: Calculate the Cladding Refractive Index (μ2)
The relative refractive index difference is defined as:
Δ=μ1−μ2μ1
Rearranging this formula to find μ2:
μ1−μ2=Δ⋅μ1
μ2=μ1−Δ⋅μ1
Substituting the values:
μ2=1.46−0.009⋅1.46
Calculating:
μ2=1.46−0.01314=1.44686≈1.45
Step 3: Calculate the Critical Angle (θc)
The critical angle can be calculated using Snell's law:
sin(θc)=μ2μ1
Substituting the values:
sin(θc)=1.451.46
Calculating:
sin(θc)≈0.9918
Now, taking the inverse sine to find θc:
θc=sin−1(0.9918)≈82.3∘
Step 4: Calculate the Numerical Aperture (NA)
The numerical aperture (NA) is given by the formula:
NA=√μ21−μ22
Substituting the values:
NA=√(1.46)2−(1.45)2
Calculating:
NA=√2.1316−2.1025=√0.0291≈0.171
Final Results
- Critical angle (θc) ≈ 82.3°
- Numerical Aperture (NA) ≈ 0.171
- Relative refractive index difference (Δ) = 0.9% = 0.009 (as a decimal)
- Core refractive index (μ1) = 1.46
- We need to find the cladding refractive index (μ2) and the critical angle (θc) at the core-cladding interface.
The relative refractive index difference is defined as:
Δ=μ1−μ2μ1
Rearranging this formula to find μ2:
μ1−μ2=Δ⋅μ1
μ2=μ1−Δ⋅μ1
Substituting the values:
μ2=1.46−0.009⋅1.46
Calculating:
μ2=1.46−0.01314=1.44686≈1.45
The critical angle can be calculated using Snell's law:
sin(θc)=μ2μ1
Substituting the values:
sin(θc)=1.451.46
Calculating:
sin(θc)≈0.9918
Now, taking the inverse sine to find θc:
θc=sin−1(0.9918)≈82.3∘
The numerical aperture (NA) is given by the formula:
NA=√μ21−μ22
Substituting the values:
NA=√(1.46)2−(1.45)2
Calculating:
NA=√2.1316−2.1025=√0.0291≈0.171
- Critical angle (θc) ≈ 82.3°
- Numerical Aperture (NA) ≈ 0.171
Similar Questions
A step index fibre has a relative refractive index difference of 0.86% Estimate the critical angle at the core-cladding interface
View SolutionA sept index fibre has a relavitive refractive index of 0.88%. What is the critical angle at the core-cladding interface?
View SolutionA silicon optical fibre with a core diameter large enough has a core refractive index of 1.50 and a cladding refrcative index 1.47.Determine(i)the critical angle at the core cladding interface.(ii)the numerical aperture for the fibre.(iii)the acceptance angle in air for the fibre.
View SolutionThe velocity of light in the core of a step index fibre 2×108m/s and the critical angle at the core-cladding interface is 80∘.Find the numerical aperture and the acceptance angle for the fibre in air.The velocity of light in vacuum is 3×108m/s
View SolutionThe glass of optical fibre has a refractive index 1.55 and cladding with another glass of refractive index 1.51. When the surrounding medium is air, the numerical aperture will be
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View SolutionFind critical angle for glass and water pair, given refractive index of glass is 1.62 and that of water is 1.33.
View SolutionLight guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media n1 and n2 as shown in the fugure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aprture (NA) of the structure is defined as sinim
If two structure of same cross-sectional area, but different numerical apertures NA1and NA2(NA2<NA1) are joined longitudinally, the numerical aperture of the combined structure is
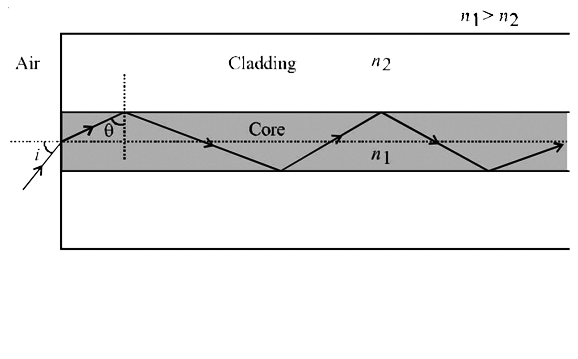
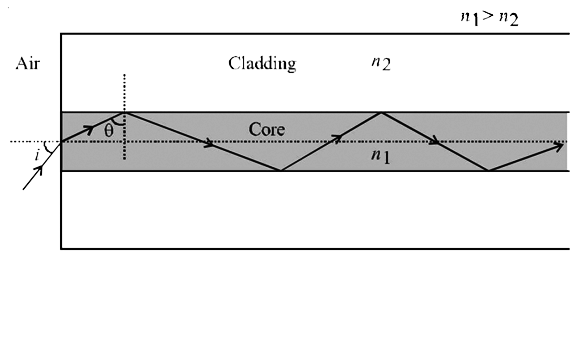
View SolutionLight guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n1 surrounded by a medium of lower refractive index n2. The light guidance in the structure takes place due to successive total internal reflectrions at the interface of the media n1 and n2 as shown in the fugure. All rays with the angle of incidence i less than a particular value im are confined in the medium of refractive index n1. The numerical aprture (NA) of the structure is defined as sinim
For two structure namely S1 with n1=√454 and n2=32, and S2 with n1=85 and n2=75 and taking the refractive index of water to be 43 and that of air to be 1, the correct option (s) is (are) ?
View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View Solution