A cabin is moving in a gravity free space along y-axis with an acceleration a. What is the time period of oscillation of a particle of mass m attached with an inextensible string of length l, in this cabin
The correct Answer is:B
To find the time period of oscillation of a particle of mass m attached to an inextensible string of length l in a cabin moving in a gravity-free space with an acceleration a, we can follow these steps:
1. Understand the Environment:
- The cabin is moving in a gravity-free space, which means the acceleration due to gravity g=0.
2. Identify the Forces:
- In the cabin, the only force acting on the mass m is the tension T in the string. Since the cabin is accelerating upwards with acceleration a, we can analyze the forces acting on the mass.
3. Apply Newton's Second Law:
- For the mass m in the cabin, the effective force acting on it can be considered as ma (due to the acceleration of the cabin). The tension in the string will provide the centripetal force required for the oscillation.
4. Relate Tension to Acceleration:
- The tension T in the string can be expressed as:
T=ma
5. Determine the Time Period of Oscillation:
- The time period T of a simple harmonic oscillator is given by the formula:
T=2π√lgeff
- In this case, since we are in a gravity-free environment, we can replace geff with the acceleration a of the cabin:
T=2π√la
6. Final Expression:
- Thus, the time period of oscillation of the particle is:
T=2π√la
Conclusion:
The time period of oscillation of the particle of mass m attached to the string of length l in the accelerating cabin is given by:
T=2π√la
- The cabin is moving in a gravity-free space, which means the acceleration due to gravity g=0.
- In the cabin, the only force acting on the mass m is the tension T in the string. Since the cabin is accelerating upwards with acceleration a, we can analyze the forces acting on the mass.
- For the mass m in the cabin, the effective force acting on it can be considered as ma (due to the acceleration of the cabin). The tension in the string will provide the centripetal force required for the oscillation.
- The tension T in the string can be expressed as:
T=ma
- The time period T of a simple harmonic oscillator is given by the formula:
T=2π√lgeff
- In this case, since we are in a gravity-free environment, we can replace geff with the acceleration a of the cabin:
T=2π√la
- Thus, the time period of oscillation of the particle is:
T=2π√la
The time period of oscillation of the particle of mass m attached to the string of length l in the accelerating cabin is given by:
T=2π√la
Similar Questions
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
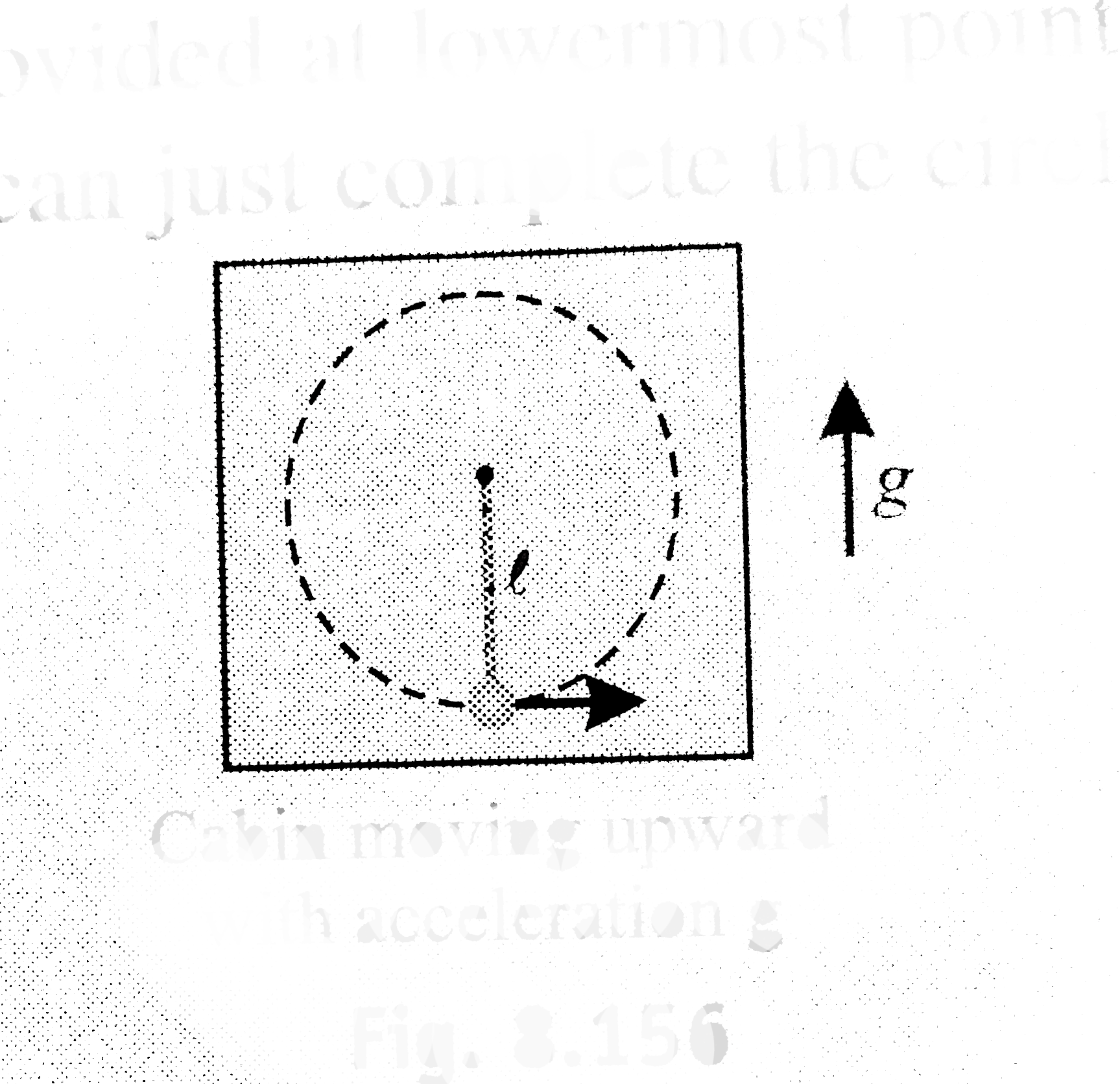
View SolutionA cabin is falling freely under gravity, what is the time period of a pendulum attached to its celling?
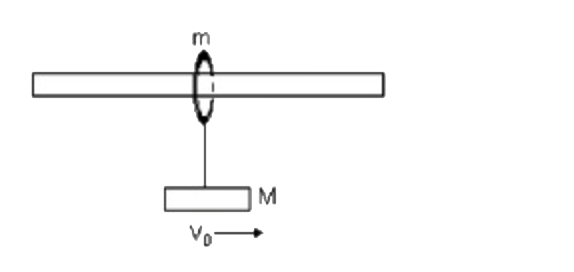
View SolutionA ring of mass m free to slide on a fixed smooth horizontal rod is attached to a particle of mass M kg by a inextensible string of length l. Initially, both M and m are at rest and the string is vertical. A horizontal velocity v0 is imparted to the particle. The maximum height up to which block will rise w.r.t its initial position is (M = 2m)
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

View SolutionThree spring mass systems are shown in figure. Assuming gravity free spece, find the time period of oscillations in each case. What should be the answer if space is not gravity free ?
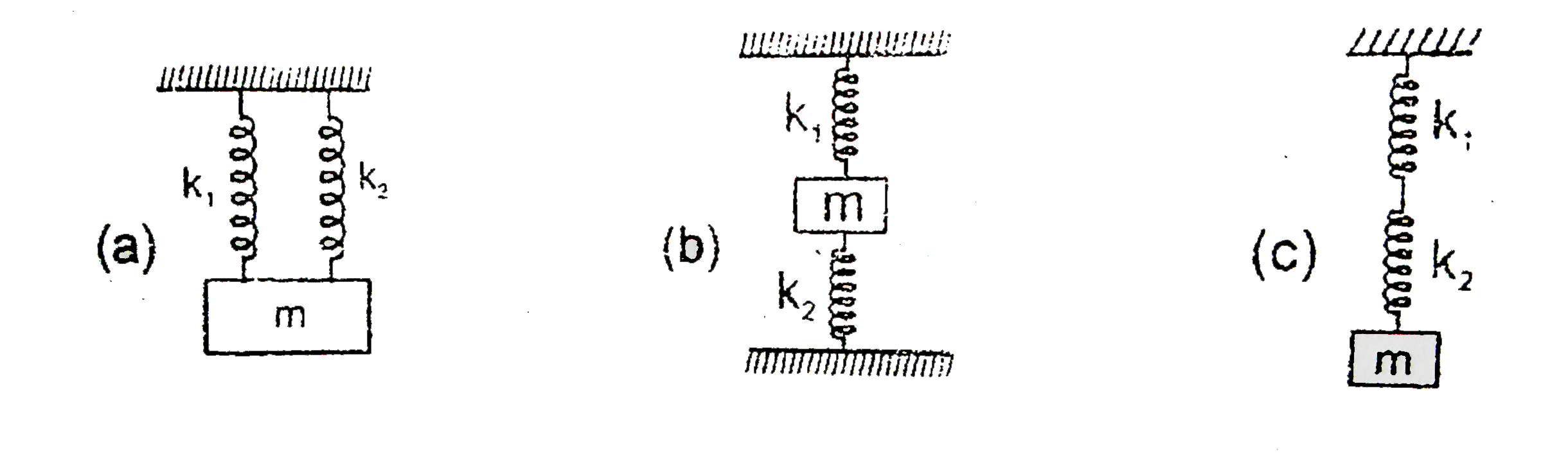
View SolutionTwo points charges are placed on x-axis as shown, a = 1 cm, q=1μC , mass of each particle m=6g. The charges are tied at the end of an inextensible string of length 2a. The whole system is free to move on a horizontal frictionless surface.

What is the tension in the string?
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View Solution