The tension at any point of the string AB will be same if

A

$\frac{\sqrt{T_{1}^{2} + T_{2}^{2}}}{2}$

B

$⎛ ⎜ ⎜ ⎝ \frac{\sqrt{T_{1}^{2} - T_{2}^{2}}}{2} ⎞ ⎟ ⎟ ⎠$

C

$⎛ ⎜ ⎜ ⎝ \frac{\sqrt{T_{1}^{2} + T_{2}^{2}}}{2} ⎞ ⎟ ⎟ ⎠$

D

none of the above.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Referring to the free budy diagrams of the bob we obtain,
$T_{1} - m g = m a$
$\Rightarrow T_{1} = m (g + a) ... (1)$
$m g - T_{2} = m a$
$\Rightarrow T_{2} = m (g - a) ... (2)$
When the cage moves horizontally with an acceleration a, the tension be T.

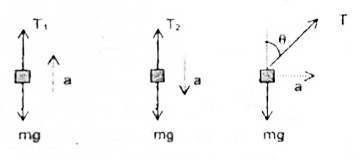
From the free body diagram, T $sin θ = m a$
And $T cos θ - m g = 0$
$\Rightarrow {(T sin θ)}^{2} + {(T - cos θ)}^{2} = {(m a)}^{2} + {(m g)}^{2}$
$\Rightarrow T^{2} = m^{2} (g^{2} + a^{2}) . . (3)$
From (1) and (2)
${(\frac{T_{1}}{m})}^{2} + {(\frac{T_{2}}{m})}^{2} = {(g + a)}^{2} + {(g - a)}^{2}$
$\Rightarrow \frac{T_{1}^{2} + T_{2}^{2}}{2} = (g^{2} + a^{2}) m^{2} ... (4)$
Equations (3) and (4), we obtain
$T^{2} = \frac{1}{2} (T_{1}^{2} + T_{2}^{2}) \Rightarrow T = \sqrt{\frac{T_{1}^{2} + T_{2}^{2}}{2}}$

Updated on:21/07/2023

|

Class 12 PHYSICS LAWS OF MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile