A bead of mass m is fitted on to a rod and can move on it without friction. At the initial moment the bead is in the middle of the rod. The rod moves translationally in a horizontal plane with an acceleration a in a direction forming an angle α with the rod. Find the acceleration of the bead relative to the rod.

Let ar be the acceleration of the bead relative to the rod. Then arcosα is the leftward horizontal acceleration of the bead relative to the rod and arsinα is downward relative acceleration of the rod. If axanday be the absolute leftward horizontal and downward vertical acceleration of the bead
arcosα−ax−a
(∵ relative acceleration is simply the vector difference between the absolute acceleration)
or, ax=arcosα+a ...(1)
and arsinα=ay−0
or, ay=arsinα ...(2)
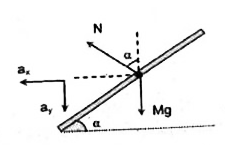
From FBD of the bead (projecting forces vertically and horizontally)
mg−Ncosα=marsinα ...(3)
and Nsinα=m(arcosα+a) ...(4)
Eliminating N between (3) and (4)
mgsinα=mar+macosα
or ar=gsinα−acosα
Similar Questions
A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
View SolutionThe rod of length l and mass m lies on a smooth floor. A ball of mass m moving horizotally with a speed u0 striked one end of rod and stick to it. After the collision, the point on the rod that moves translationally ( without any rotation) in the previous direction of motion of the ball.

A. Is the centre of C of the rod.
B. Is the left end A of the rod.
C. Lies at a distance l/4 to the left of point C
D. Lies at a distance l/4 to the right of point C.
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
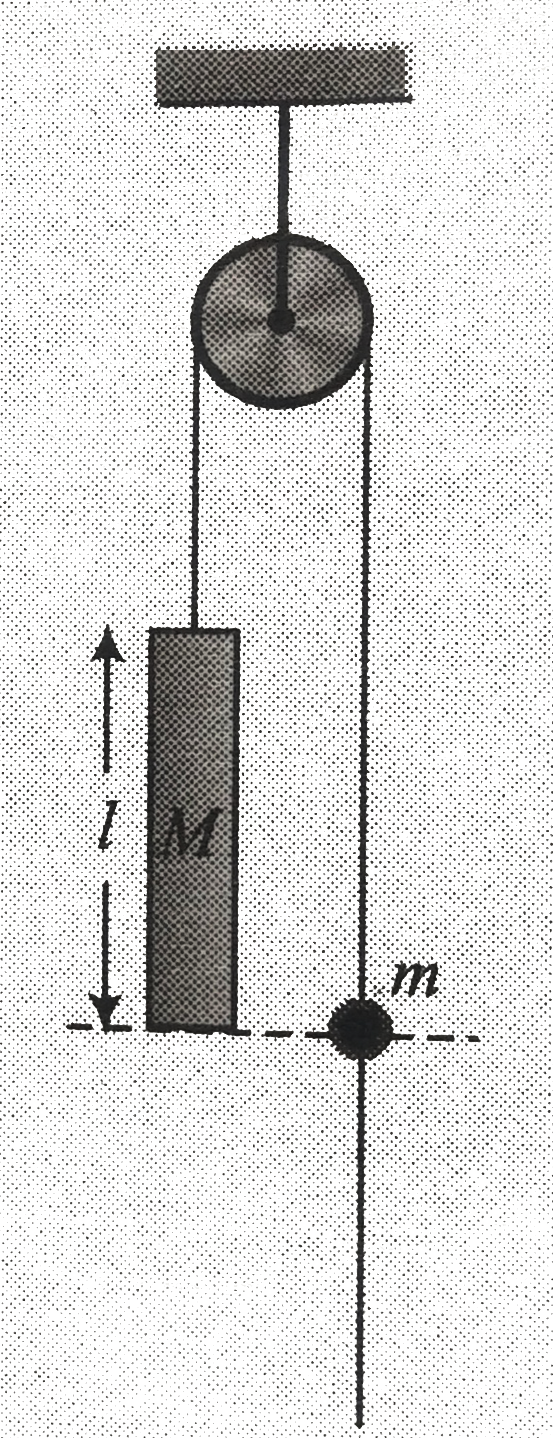
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
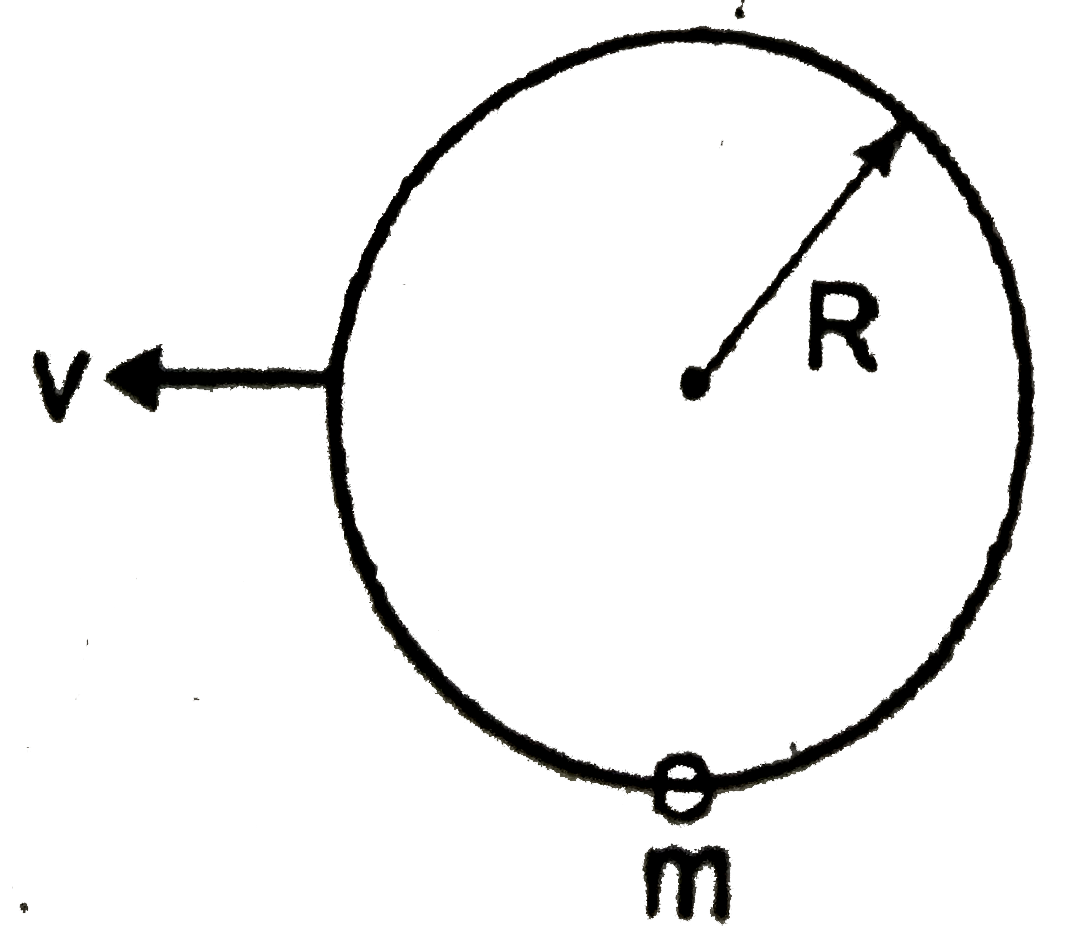
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

A. the normal reaction on the bead will be constant h magnitude and direction both
B. the magnitude of the normal reaction on the bead will be variable
C. the magnitude of friction force on the bead will be constant
D. the magnitude of friction force on the bead will be variable
View SolutionA rod of mass 'm and length L is attached to a L shaped plank at 'A'. rod can move freely about A. A string is tied between rod and plank as shown in figure. Whole system is moving with a constant acceleration g in x-direction
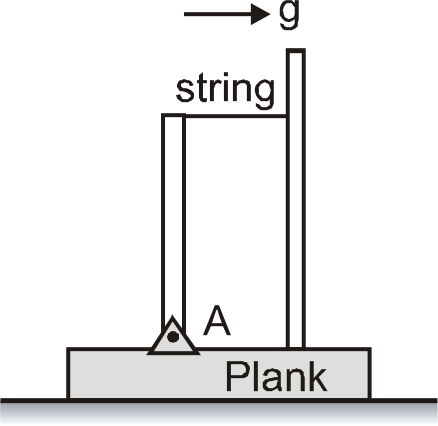
Force exerted by hinge on the rod is
View Solution

