A man of mass m climbs a rope of length L suspended below a balloon of mass M. The balloon is stationary with respect to ground. If the man begins to climb up the rope at a speed vrel. (relative to rope) in what direction and with what speed (relative to gound) with the balloon move ?
The change in momentum Δp of the ball during Δ=0.01 sec is known as the impulse (FΔt) of the force of impact
⇒FΔt=Δp
|Δ→p|=|m→v2−m→v1|=m(v1+v2)
∵m→v1&m→v2 are antiparallel
⇒Fδt=m(v1+v2) ...(1)
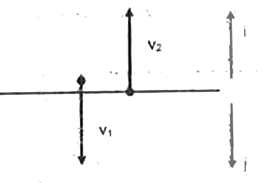
Since, the ball falls through a height h, and its velocity just before striking the surface is √2gh. As the ball losses 75percent of its total mechanical energy that is knetic energy.
⇒1/2mv22=1/2mv21(1−75/100)
⇒v2=v12=√2gh2=√gh2
Substitution of the values of v1 and v2 in (1) yields
FΔt=50×10−3×3√gh2=50×10−3×3√(9.8)(10)2=1.05 N - sec.
Similar Questions
A man of mass m climbs to a rope ladder suspended below a balloon of mass M. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed v (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
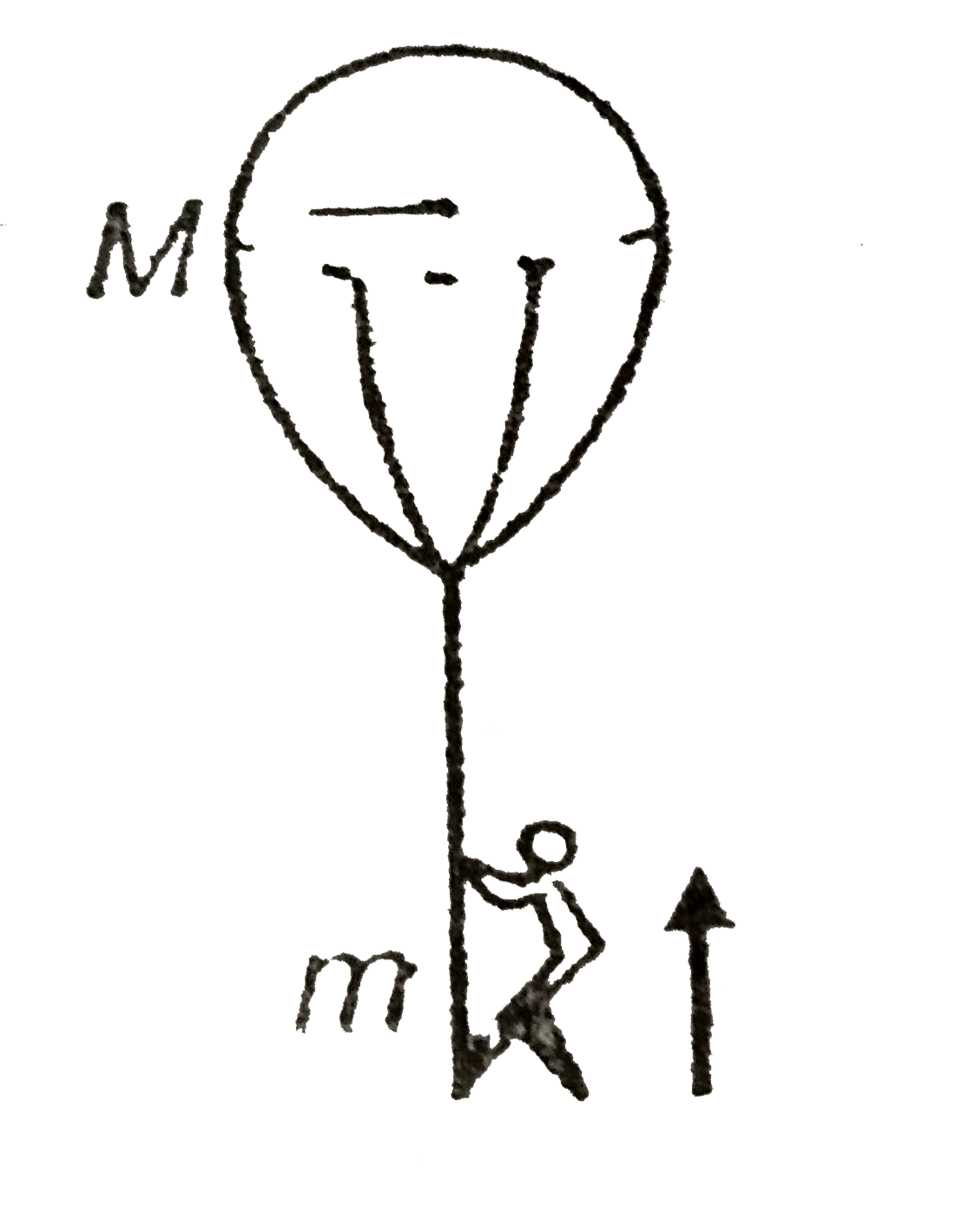
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
View SolutionA man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velocity relative to the ice does the platform recoil?
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionA man of mass m moves with a constant speed on a plank of mass M and length l kept initially at rest on a frictionless horizontal surface, from one end to the other in time t. The speed of the plank relative to grounud while man is moving, is
View SolutionA man of mass m moves with a constant speed on a plank of mass M and length L kept initially at rest on a frictionless horizontal surface . From one end to the other he reaches in time t . The speed of the plank relative to ground while man is moving , is
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
View SolutionA man of mass m slides down along a rop which is connected to the celling of an elevator with deceleration a relative to the rop.If the elevator is going upward with an acceleration relative to the ground, then tension in the rop is
View SolutionA man in a balloon throws a stone downwards with a speed of 5m/s with respect to balloon. The balloon is moving upwards with a constant acceleration of 5m/s2. Then velocity of the stone relative to the man after 2 seconds is.

View Solution