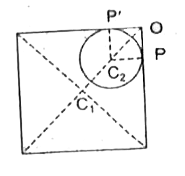
A disc of radius R is placed on a square plate of edge 4R made up of the same sheet with their planes parallel such that any two adjacent sides ofsquare touch the disc. Find the distance of the centre of mass of the system from the centre of square plate?
Let us consider that σ = mass / area of the sheet
Mass of disc =m1=πR2σ & mass of square plate =16R2σ
By geometry OP. = OP = R
C1C2=2√2R−√2R=√2R
∴Xcm=√2R×πR2σ+0×16R2σ(16+π)R2σ=√2πR16+π along
C1C2 from C1
Similar Questions
Centre of mass of the system lies inside disc or square plate and why ?
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View SolutionA square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of square.

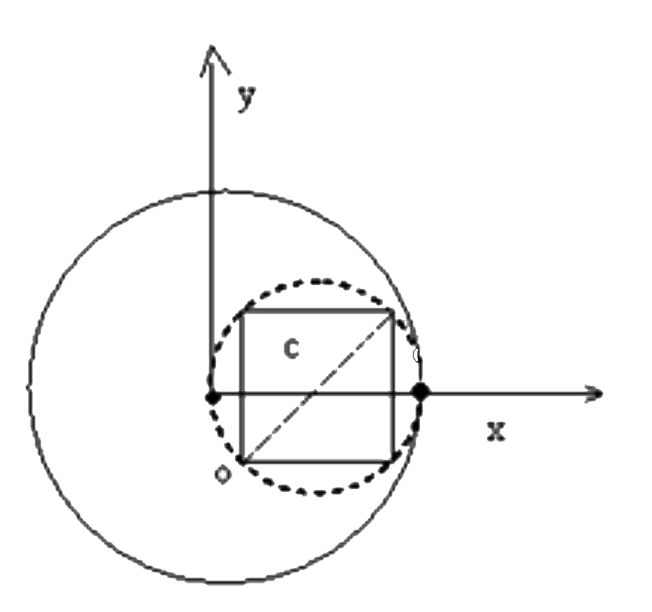
View SolutionThere is a thin uniform disc of radius R and mass per unit area σ in which a hole of radius R/2 has been cut out as shown in the figure. Inside the hole, a square plate of same mass per unit area σ is inserted so that its corners touch the periphery of the hole. The distance of the centre of mass of the system from the origin is
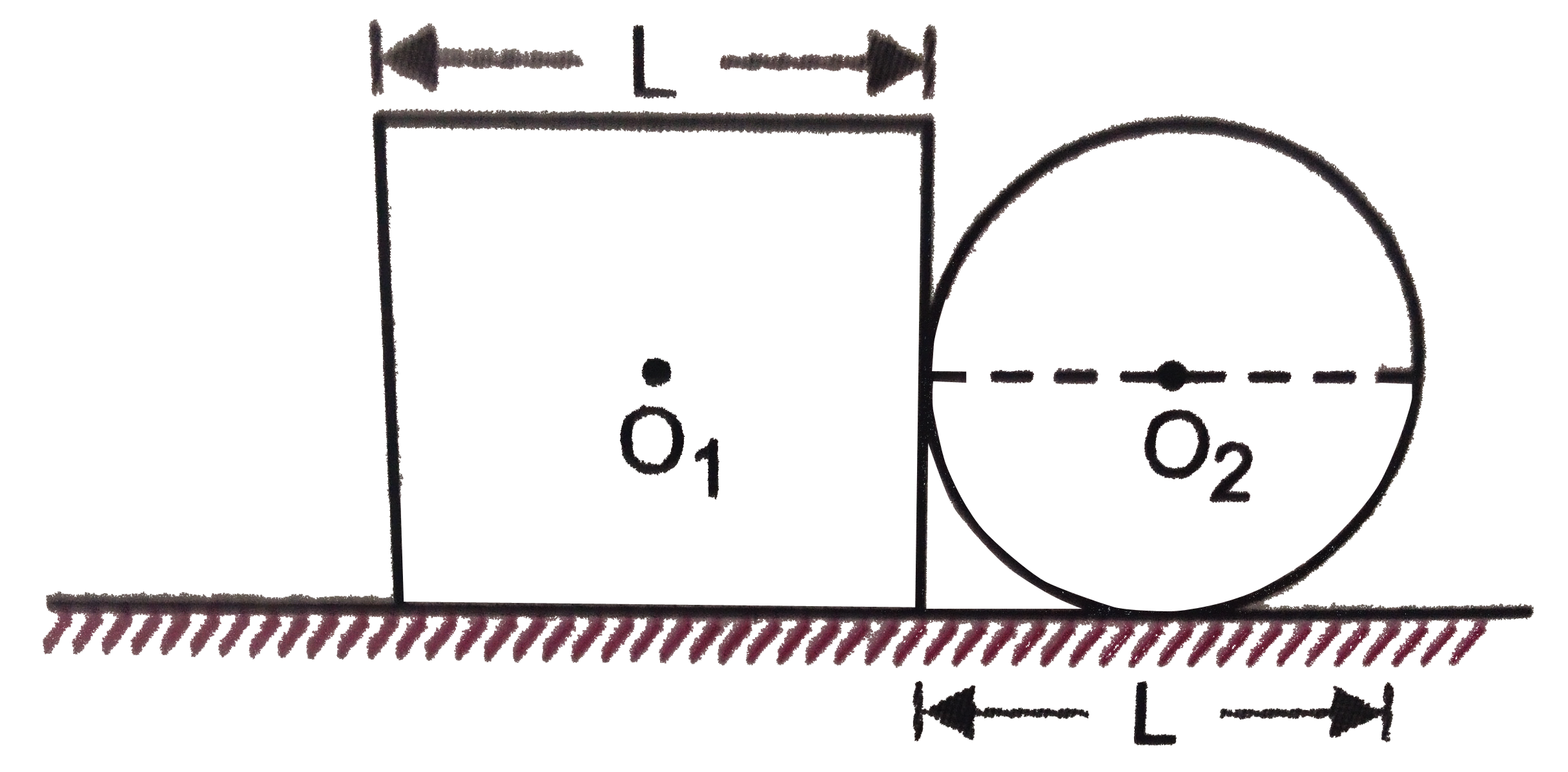
View SolutionA uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to L. Locate the position of centre of mass of the system w.r.t. the centre of the square.
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View Solution

