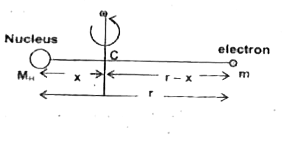
The angular momentum of the atom will be constant about an axis passing through
u
8mu(8m+M)
8mu8m+3M
8mu8m+3M
The correct Answer is:C
v=ω(2R)=8μ(8m+3M)
Similar Questions
A particle of mass m is projected with a speed v at an angle θ with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
(a) When the particle is at maximum height and
(b) When the particle is just about to collide with the horizontal surface
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View Solution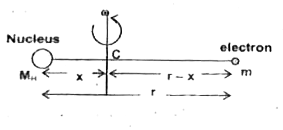
The angular momentum of the atom about the centre of mass will be
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View SolutionA wheel of moment of inertia 2kgm2 is rotating about an axis passing through centre and perpendicular to its plane at a speed 60rad/s. Due to friction, it comes to rest in 5 minutes. The angular momentum of the wheel three minutes before it stops rotating is
View SolutionA hydrogen atom is in a state with energy −1.51eV. in the Bohr model, what is the angular momentum of the electron in the atom with respect to an axis at the nucleus?
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionA : If angular momentum of an object is constant about a point then net torque on it about that point is zero.
R : Torque is equal to the rate of change of angular momentum.
View SolutionIf two charged particles each of charge q mass m are connected to the ends of a rigid massless rod and is rotated about an axis passing through the centre and ⊥ to length. Then find the ratio of magnetic moment to angular momentum
View Solution
