A planet of mass $m$ revolves in elliptical orbit around the sun of mass $M$ so that its maximum and minimum distance from the sun equal to $r_{a}$ and $r_{p}$ respectively. Find the angular momentum of this planet relative to the sun.

Video Solution

Text Solution

Verified by Experts

The angular momentum
$L = m v r$ ……… $(1)$
Conservation of angular momenta at point $1$ and $2$ ,
$m v_{1} r_{1} = m v_{2} r_{2}$
$\Rightarrow v_{1} r_{1} = v_{2} r_{2}$ ……….. $(2)$
Conservation of energy at $1$ and $2$
$\frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}}$ .......... $(3)$
Using equation $(2)$ and $(3)$ we obtain
$v_{1} = \sqrt{2 G M (\frac{1}{r_{1}} - \frac{1}{r_{2}}) + v_{2}^{2}}$
$\Rightarrow v_{1} = \sqrt{2 G M (\frac{1}{r_{1}} - \frac{1}{r_{2}}) + {(\frac{v_{1} r_{1}}{r_{2}})}^{2}}$
$\Rightarrow v_{1}^{2} [1 - {(\frac{r_{1}}{r_{2}})}^{2}] = 2 G M (\frac{r_{2} - r_{1}}{r_{1} r_{2}})$
$\Rightarrow v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}}$
$∴ L = m v_{1} r_{1} = m \sqrt{\frac{2 G M r_{1} r_{2}}{r_{1} + r_{2}}}$

Updated on:21/07/2023

|

Class 12 PHYSICS GRAVITATION

Similar Questions

Knowledge Check

A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

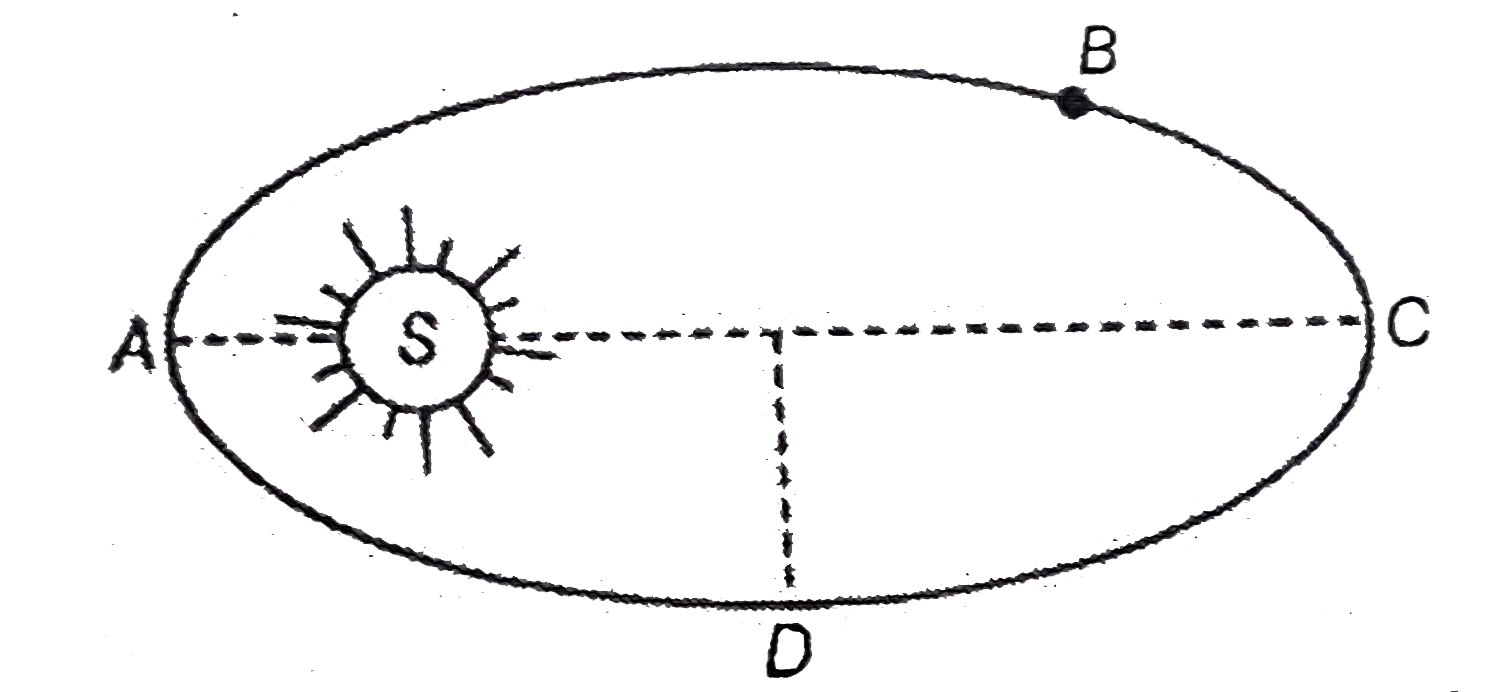AA
BB
CC
DD

Recommended Questions

Home
Ask Doubt
Profile