Question

Space junk of mass $m$ leaves its orbit and heads towards on annular disc-shaped meteor at rest relative to earth along its axis at a distance $8R$ with a velocity $v$. The surface mass density of the meteor is $\sigma$ and its inner and outer radii are $R$ and $4R$. Find the velocity with which the junk passes the centre of the meteor. (Thickness of the meteor is negligible).

Explanation

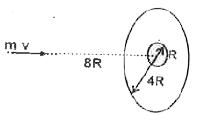
Consider an elemental ring of radius `r` and width `dr`.
We have potential energy of the system (ring `+` junk)
`dE_(1)=-(Gmdm)/((x^(2)+r^(2))^(1//2))=(GM2pidr sigma)/((x^(2)+r^(2))^(1//2))`
`E_(1)=-2piGm sigma int_(R_(1))^(R_(2))(rdr)/((x^(2)+r^(2))^(1//2))`
Substituting , `x^(2)+r^(2)=t`
`2rdr=dt`, `rdr=dt//2`
`E_(1)=-2piGmsigma int(dt)/(2(t)^(1//2))=-2piGmsigma|(x^(2)+r^(2))^(1//2)|_(R_(1))^(R_(2))`
`=-2piGmsimga[(x^(2)+R_(2)^(2))^(1///2)-(x^(2)+R_(1)^(2))^(1//2)]`.........`(i)`
Ath the centre `E_(2)=-2piGmsigma(R_(2)-R_(1))`.........`(ii)`
The initial kinetic energy of the junk `E_(3)=(1)/(2)mv^(2)`
Let the velocity of the junk at the centre be `v.` then `E_(4)=(1)/(2)Mv^(2)`
Conserving energy, `E_(1)+E_(3)=E_(2)+E_(4)`
`implies-2piGmsigma[(x^(2)+R_(2)^(2))^(1//2)-(x^(2)+R_(1)^(2))^(1//2)]+(1)/(2)mv^(2)=-2piGmsigma(R_(2)-R_(1))+(1)/(2)mv^(2)`
`implies-2piGsigma[(64R^(2)+16R^(2))^(1//2)-(64R^(2)+R^(2))^(1//2)]+(1)/(2)v^(2)=-2piGsigma(3R)+(1)/(2)v.^(2)`
`impliesv.={4piGsigma[3-sqrt(5)(4-sqrt(13))]R+v^(2)}^(1//2)`