Air flows horizontally with a speed v = 108 km/hr . A house has a plane roof of area A = 20 m2 . Find the magnitude of aerodynamic lift on the roof . [ Density of air =1.3kg/m3]
To find the magnitude of aerodynamic lift on the roof of the house, we can use Bernoulli's theorem. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have air flowing horizontally over a plane roof. The speed of the air is given, and we need to find the lift force acting on the roof due to the difference in pressure above and below the roof.
Step 2: Identify Given Values
- Speed of air, v=108km/hr
- Area of the roof, A=20m2
- Density of air, ρ=1.3kg/m3
Step 3: Convert Speed to SI Units
Convert the speed from kilometers per hour to meters per second:
v=108km/hr×1000m1km×1hr3600s=30m/s
Step 4: Apply Bernoulli's Equation
According to Bernoulli's theorem, the pressure difference (ΔP) between the top and bottom of the roof can be expressed as:
ΔP=12ρv2
Here, v is the speed of air above the roof, and the speed below the roof is zero (since it is at rest).
Step 5: Calculate the Pressure Difference
Substituting the values into the equation:
ΔP=12×1.3kg/m3×(30m/s)2
Calculating this gives:
ΔP=12×1.3×900=585Pa
Step 6: Calculate the Lift Force
The lift force (F) acting on the roof can be calculated using the area of the roof:
F=ΔP×A
Substituting the values:
F=585Pa×20m2=11700N
Step 7: Final Result
The magnitude of aerodynamic lift on the roof is approximately:
F≈1.17×104N
We have air flowing horizontally over a plane roof. The speed of the air is given, and we need to find the lift force acting on the roof due to the difference in pressure above and below the roof.
- Speed of air, v=108km/hr
- Area of the roof, A=20m2
- Density of air, ρ=1.3kg/m3
Convert the speed from kilometers per hour to meters per second:
v=108km/hr×1000m1km×1hr3600s=30m/s
According to Bernoulli's theorem, the pressure difference (ΔP) between the top and bottom of the roof can be expressed as:
ΔP=12ρv2
Here, v is the speed of air above the roof, and the speed below the roof is zero (since it is at rest).
Substituting the values into the equation:
ΔP=12×1.3kg/m3×(30m/s)2
Calculating this gives:
ΔP=12×1.3×900=585Pa
The lift force (F) acting on the roof can be calculated using the area of the roof:
F=ΔP×A
Substituting the values:
F=585Pa×20m2=11700N
The magnitude of aerodynamic lift on the roof is approximately:
F≈1.17×104N
Similar Questions
Knowledge Check
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103N
The speed of the wind passing over the wings of a small aeroplane is 70 m/s and below the wing is 60 m/s. If the mass of the plane is 1000 kg and the area of wing is 14m2, then what will be ther net vertical force on the aeroplane ?
? (Density of air =1.2kg/m3andg=10m/s2)
View SolutionThe speed of flow past the lower surface of a wing of an aeroplane is 50ms−1. What speed of flow over the upper surface will give a dynamic lift of 1000pa? Density of air =1.3kgm−3
View SolutionFigure shows a crude type of atomizer. is compressed, air flows swiftly through tube BC causing a reduced pressure in the particles of the vertical to Liquid rises in the tube, enters BC and is sprayed out. if the pressure in the bulb is Pa+P, where P is the gauge pressure and Pa is the atmospheric pressure, v is the speed of air in BC, find how large would v need to be to cause the liquid to rise to BC. Density of air =1.3kg/m3.
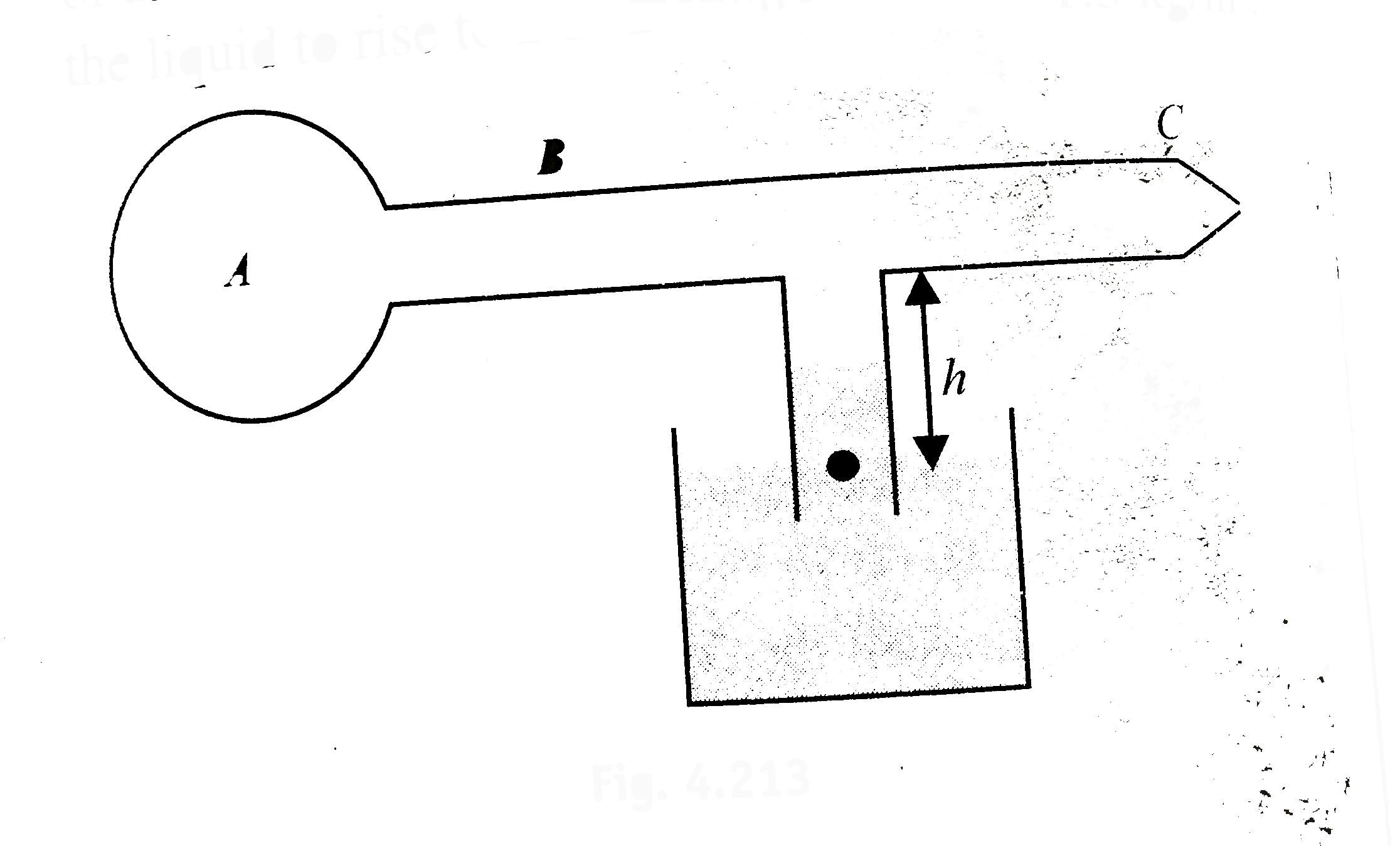
View SolutionA stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionAir stream flows horizontally past an aeroplane wing of surface area 4m2. The speed of air over the top surface is 60ms−1 and under the bottom surface is 40ms−1 The force of lift on the wing is (density of air =1kgm−3)
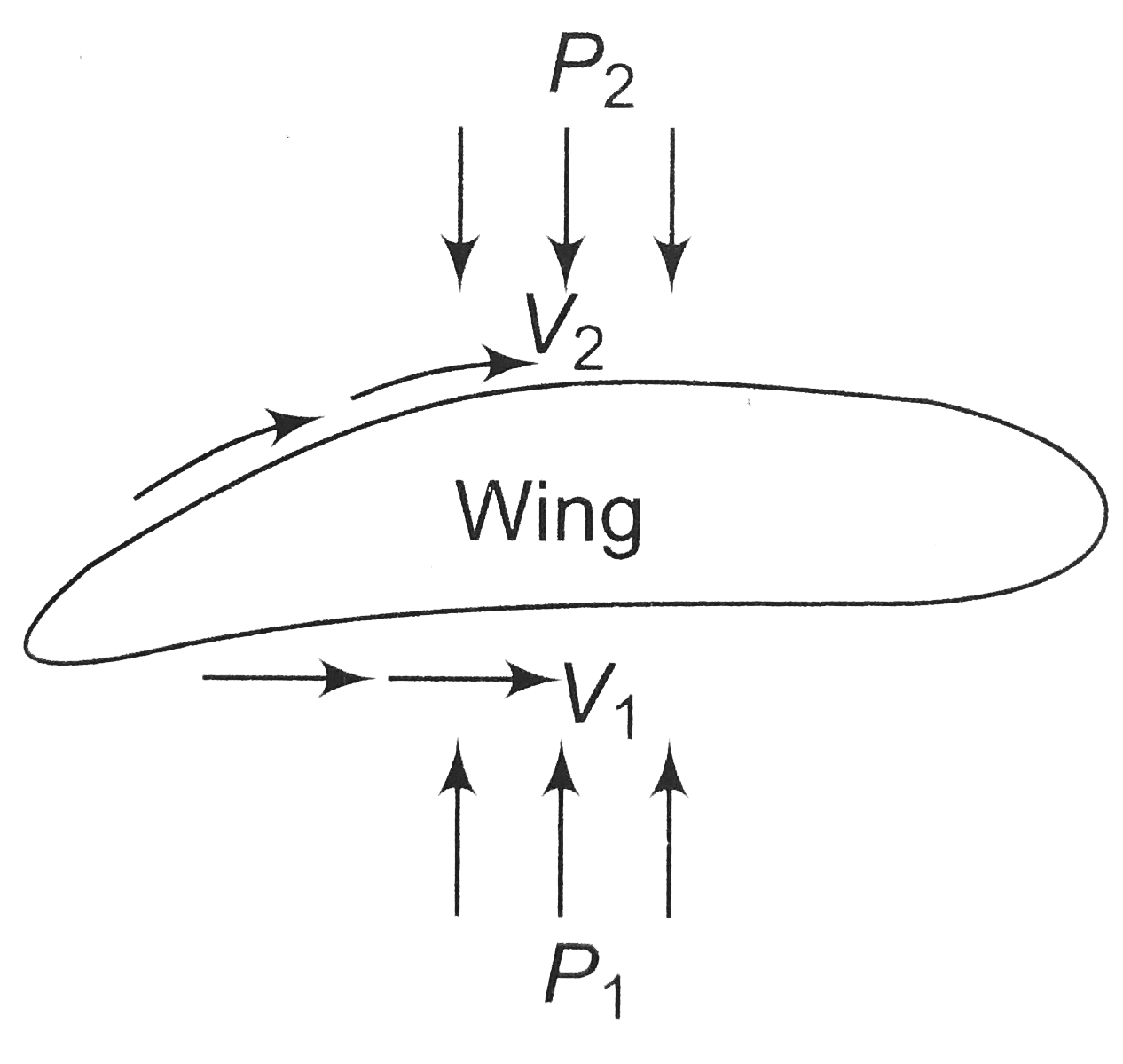
View SolutionAir flows over the top of an aeroplane wing of area A with speedv1 and past the under side of the wing of area A with speed v2 Show that the magnitude of the upward in force on the wing L is L = 12ρA(v21−v22) where ρ is the density of the alr.
View SolutionAir streams horizontally past an air plane. The speed over the top surface is 60 m/s, and that under the bottom surface is 45 m/s. The density of air is 1.293 kg/m3, then the difference in pressure
View Solution

