The vertical arms of U - tube have unequal raidus R and r (R>r) . If a liquid of surface tension T and density ρ rests in equillibrium inside the U - tube , find the level difference h between the meniscuses in the two arms .
To solve the problem of finding the level difference h between the meniscuses in the two arms of a U-tube with unequal radii R and r (where R>r), we will follow these steps:
1. Understanding the System:
- We have a U-tube with two vertical arms. The left arm has a radius r and the right arm has a radius R. A liquid with surface tension T and density ρ is in equilibrium inside the U-tube.
2. Pressure at the Meniscus:
- The pressure at the liquid surface in the left arm (smaller radius) can be expressed as:
P1=Patm−2Tr
- The pressure at the liquid surface in the right arm (larger radius) can be expressed as:
P2=Patm−2TR
3. Equilibrium Condition:
- At the point where the liquid is in equilibrium, the pressure difference between the two arms must balance the hydrostatic pressure difference due to the height h:
P1+ρgh=P2
4. Substituting Pressures:
- Substitute P1 and P2 into the equilibrium equation:
(Patm−2Tr)+ρgh=(Patm−2TR)
5. Simplifying the Equation:
- Cancel Patm from both sides:
−2Tr+ρgh=−2TR
- Rearranging gives:
ρgh=2TR−2Tr
6. Factor Out Common Terms:
- Factor out 2T:
ρgh=2T(1R−1r)
7. Solving for h:
- Finally, solve for h:
h=2Tρg(1R−1r)
Final Result:
The level difference h between the meniscuses in the two arms of the U-tube is given by:
h=2Tρg(1R−1r)
- We have a U-tube with two vertical arms. The left arm has a radius r and the right arm has a radius R. A liquid with surface tension T and density ρ is in equilibrium inside the U-tube.
- The pressure at the liquid surface in the left arm (smaller radius) can be expressed as:
P1=Patm−2Tr
- The pressure at the liquid surface in the right arm (larger radius) can be expressed as:
P2=Patm−2TR
- At the point where the liquid is in equilibrium, the pressure difference between the two arms must balance the hydrostatic pressure difference due to the height h:
P1+ρgh=P2
- Substitute P1 and P2 into the equilibrium equation:
(Patm−2Tr)+ρgh=(Patm−2TR)
- Cancel Patm from both sides:
−2Tr+ρgh=−2TR
- Rearranging gives:
ρgh=2TR−2Tr
- Factor out 2T:
ρgh=2T(1R−1r)
- Finally, solve for h:
h=2Tρg(1R−1r)
The level difference h between the meniscuses in the two arms of the U-tube is given by:
h=2Tρg(1R−1r)
Similar Questions
A tube of radius r and sufficient height is dipped in a liquid of surface tension S and density ρ. Heat developed upto steady state will be
Note: θ is the contact angle
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?
View SolutionChoose the correct option:
A capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
The work done by surface tension will be
View SolutionA U−tube is made up of capillaries of bores 1mm and 2mm respectively. The tube is held vertically and partically filled with a liquid of surface tension 49dyne/cm and zero contact angle. Calculate the density of the liquid of the difference in the levels of the meniscus is 1.25cm.
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View SolutionIf the time period (T)of vibration of a liquid drop depends on surface tension (S) , radius(r) of the drop , and density (ρ) of the liquid , then find the expression of T.
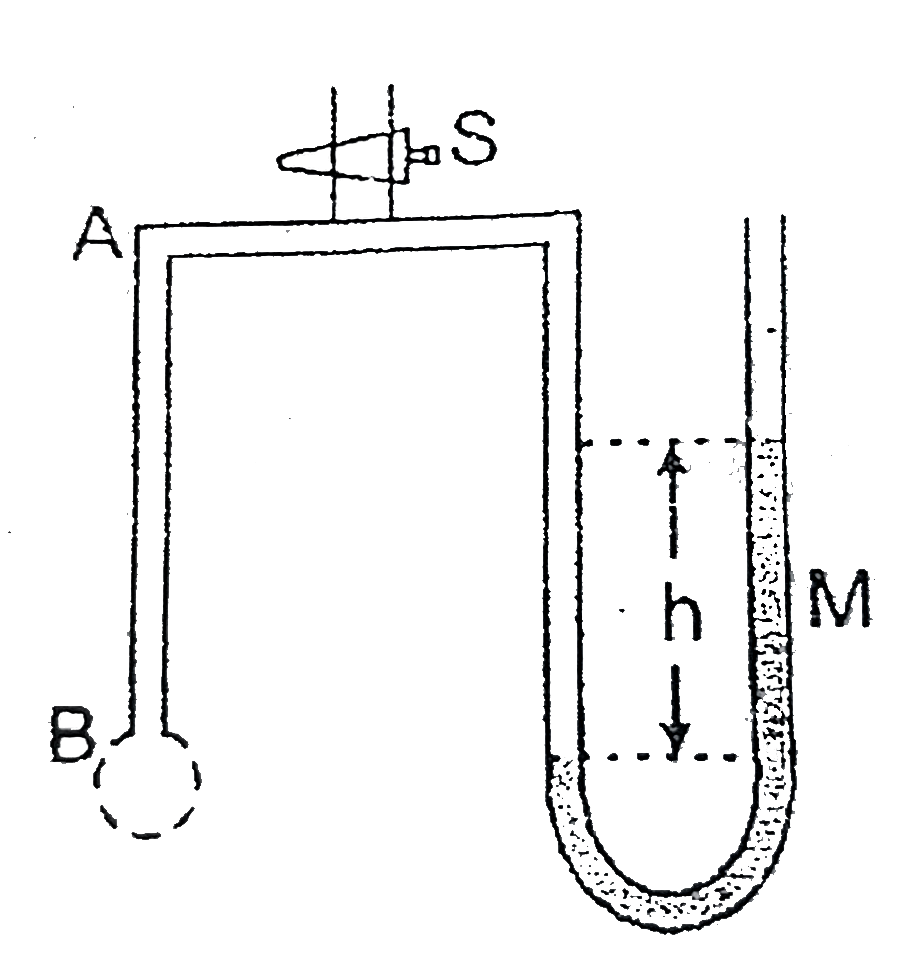
View SolutionA tube of fine bore AB is connected to a manomeer M as shown. The stop cock S controls the flow in air. AB is dipped into a liquid whosw surface tension is σ. On opening the stop cock for a while, a bubble is formed at B and the manometer level is recorded, showing a difference h in the levels in the two arms. If ρ be the density of manometer liquid and r the radius of curvature of the bubble, then the surface tension σ of the liquid is given by
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -
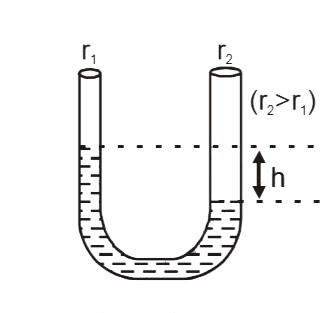
View SolutionA U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
View SolutionA vertical U-tube of uniform cross-section contains water jn both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. The level difference between the two free surfaces in the two limbs wiil be
View Solution

