A circular ring of small thickness and of inner and outer diameters 3.8 cm and 4.2 cm respectively , suspended on one side of a common balance is exactly balanced by keeping sufficient mass in the pan on other side .At this instant the lower surface of ring is just resting on the surface of a liquid . Now if the ring is puled up gently , such that it does not loose its contact with the liquid , find how much mass should be changed in other pan , again to keep the balance in balanced position ? (Assume angle of contact is zero and surface tension of liquid is (1/π) N/m)
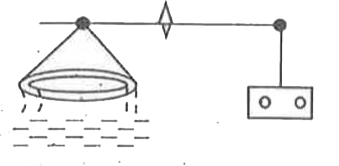
Total force due to surface tension =(2πr1+2πr2)T
mg=2πT(r1+r2)
m=2πT(r1+r2)g=2π×10π×103(2+2.2)1000=8gm
Similar Questions
Find the area of a triangle whose sides are 3cm, 4cm and 5cm respectively.
View SolutionThe inner and outer diameters of ring 1 of a dartboard are 32cm and 34cm respectively and those of rings II are 19cm and 21cm respectively. What is the total area of these two rings?
View SolutionThe longest side of a right angled triangle is 4cm longer than one side and 2 cm longer than the other side. Find the longest side.
View SolutionA circular conducting ring is rotated about one of its diameter in a magnetic field
View SolutionA hollow cylindrical pipe is 21 dm long. It outer and inner diameters are 10cm and 6cm respectively. Find the volume of the copper used in making the pipe.
View SolutionFind the area of a ring whose outer and inner radii are respectively 20 cm and 15 cm
View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.

View SolutionA circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
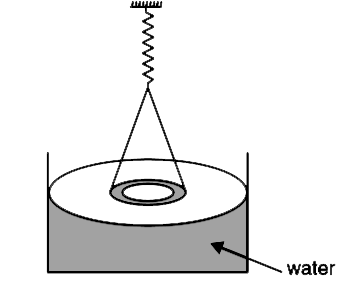
View SolutionA ring of internal and external diameters 8.5×10−2m and 8.7×10−2m is supported horizontally from the pan of a physical balance such that it comes in contact with a liquid. An extra force of 40N is required to pull it away from the liquid . Determine the surface tension of the liquid?
View SolutionThe hypotenuse of a triangle is 2.5 cm. If one of the sides is 1.5 cm. find the length of the other side.
View Solution

