A tug, exerting a pulling force of 800 N due north, tows a barge through a distance of 1 km in a direction 30∘E of north. What is the work done by the tug?
To find the work done by the tug, we can follow these steps:
Step 1: Identify the force and the distance
The tug exerts a pulling force of F=800N in the north direction. The barge is towed through a distance of d=1km=1000m at an angle of 30∘ east of north.
Step 2: Break down the distance vector into components
We need to resolve the distance vector into its components. The distance vector r can be expressed as:
r=d⋅(sin(30∘)cos(30∘))
Substituting d=1000m:
r=1000⋅(sin(30∘)cos(30∘))
Step 3: Calculate the components of the distance vector
Using the trigonometric values:
- sin(30∘)=12
- cos(30∘)=√32
Thus, we have:
r=1000⋅⎛⎝12√32⎞⎠=(500500√3)m
Step 4: Write the force vector
The force vector F can be expressed as:
F=(0800)N
Step 5: Calculate the work done using the dot product
The work done W is given by the dot product of the force and distance vectors:
W=F⋅r=(0800)⋅(500500√3)
Calculating the dot product:
W=0⋅500+800⋅500√3=400000√3J
Step 6: Convert to kilojoules
To convert to kilojoules:
W=400√3kJ
Using √3≈1.732:
W≈400⋅1.732≈692.8kJ
Final Answer
The work done by the tug is approximately 692.8kJ.
---
The tug exerts a pulling force of F=800N in the north direction. The barge is towed through a distance of d=1km=1000m at an angle of 30∘ east of north.
We need to resolve the distance vector into its components. The distance vector r can be expressed as:
r=d⋅(sin(30∘)cos(30∘))
Substituting d=1000m:
r=1000⋅(sin(30∘)cos(30∘))
Using the trigonometric values:
- sin(30∘)=12
- cos(30∘)=√32
r=1000⋅⎛⎝12√32⎞⎠=(500500√3)m
The force vector F can be expressed as:
F=(0800)N
The work done W is given by the dot product of the force and distance vectors:
W=F⋅r=(0800)⋅(500500√3)
Calculating the dot product:
W=0⋅500+800⋅500√3=400000√3J
To convert to kilojoules:
W=400√3kJ
Using √3≈1.732:
W≈400⋅1.732≈692.8kJ
The work done by the tug is approximately 692.8kJ.
Similar Questions
A force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View Solution
Knowledge Check
Which of the following figure represents the force of 10N in a direction of 30∘ east of north?
A B
B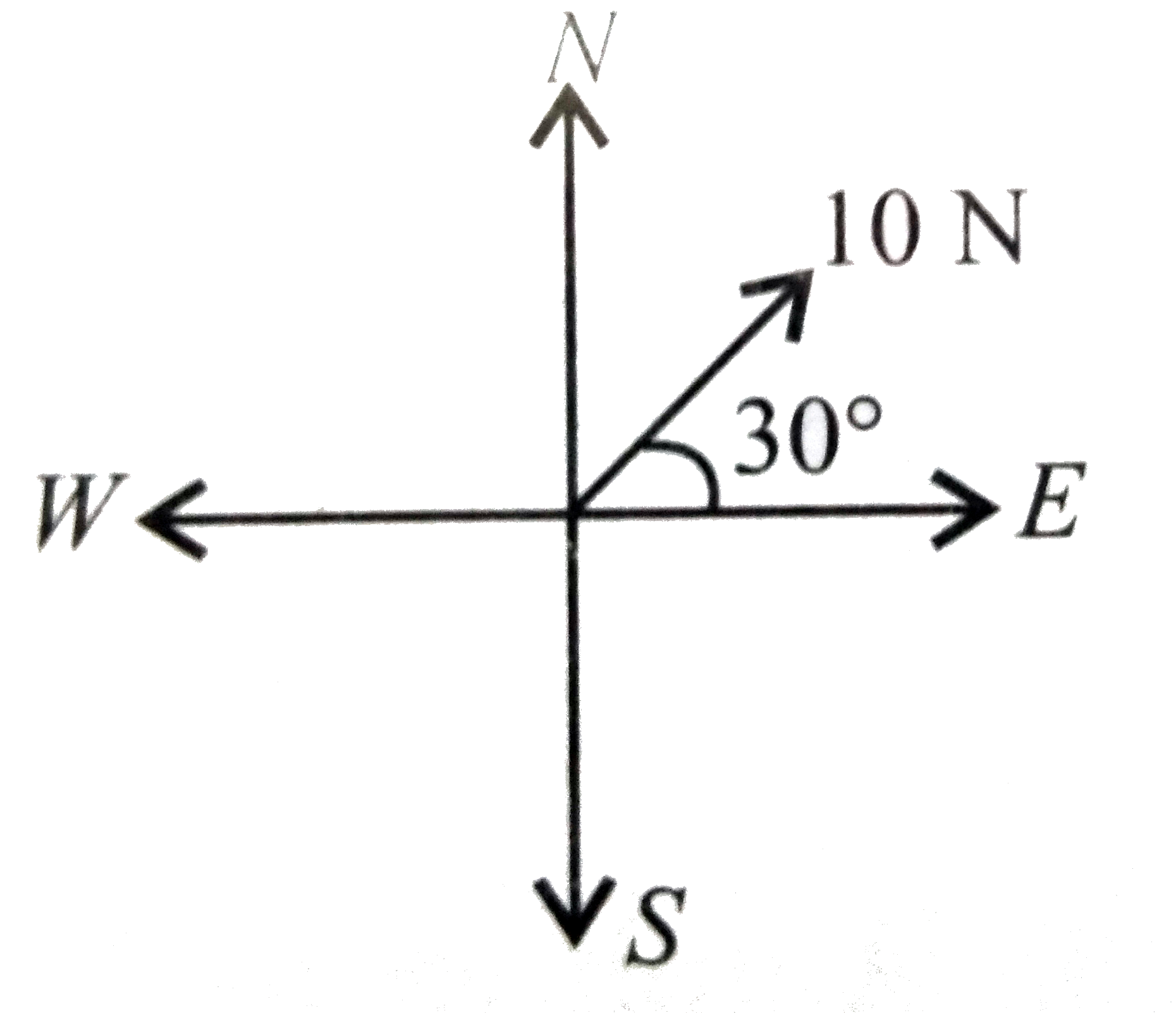 C
C D
D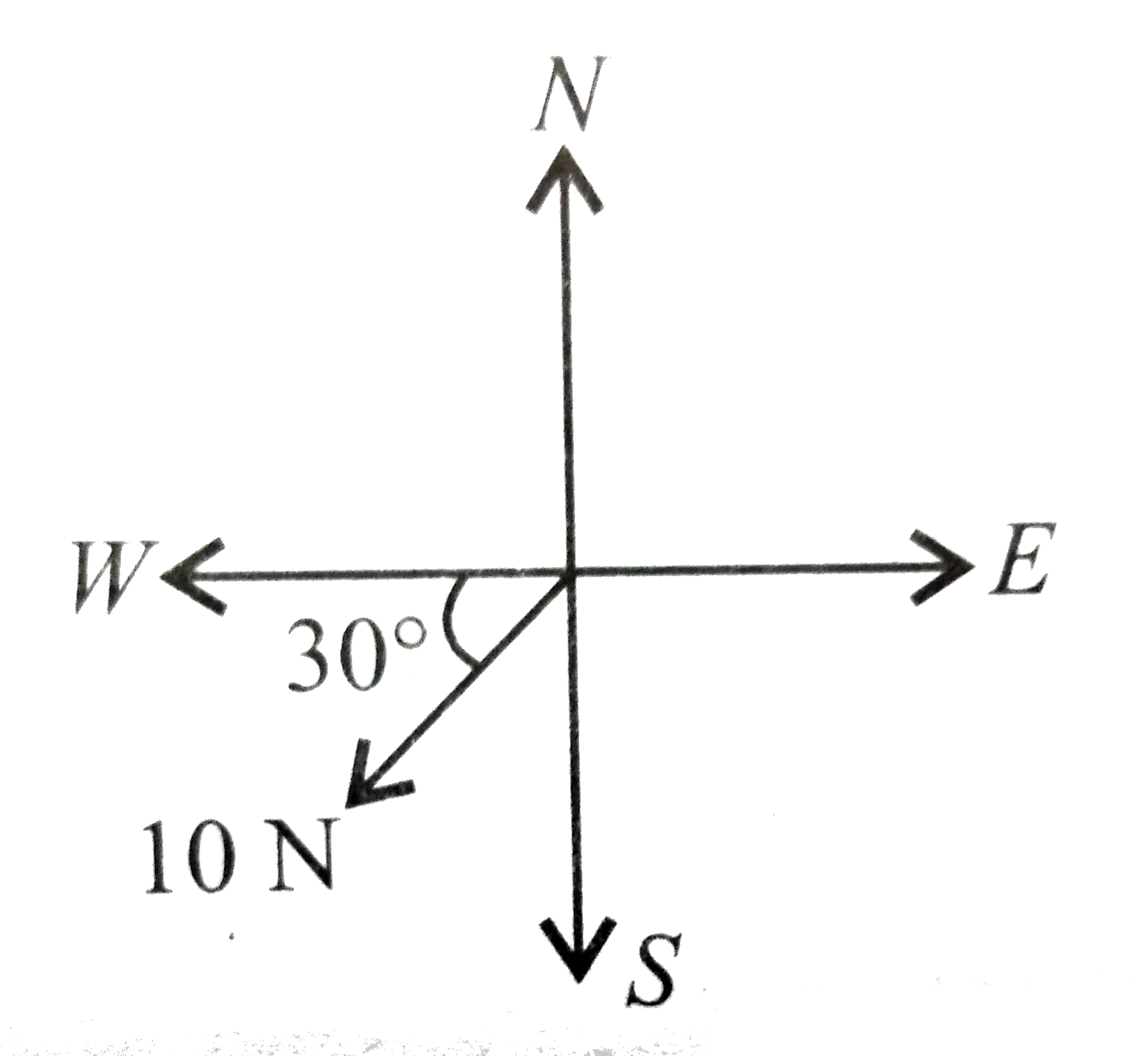
A force of 10 N displaces a body by a distance of 2 m at an angle 60∘ to its own direction. Find the amount of work done.
View SolutionA force of 25 N causes a displacement of 4 m in its own direction. What is the magnitude of work done ?
View SolutionHow much force is applied on the body when 780 J of work is done in displacing the body through a distance of 30 m in the direction of force?
View SolutionFind the work done if a force of 1000 N is applied on a load and the load moves through a distance of 50 cm.
View SolutionA boy does a work of 800 J is dragging a sach of rice through a distance of 10 m. what is the magnitude of force applied by the boy?
View SolutionA person pushes a box on a rough horizontal plateform surface.He applies a force of 200 N over a distance of 15 m. Therefore, he gets progressively tired and his applied force reduces linearly with distance to 100 N. The total distance through which the box has been moved is 30 m. What is the work done by the person during the total movement of the box?
View SolutionA block A, weighing 100 N is pulled up a slope of length 5 m by means of a constant force F (= 100 N) as illustrated in Fig.

(a) What is the work done by the force F in moving the block A 5 m along the slope ?
(b) What is the increase in potential energy of the block A?
(c) Account for the difference in the work done by the force and the increase in potential energy of the block
View Solution
