A small block is projected with a speed v0 on a horizontal track placed on a sufficiently rough surface which turns into a semi circle ( vertical) of radius R. Find the min value of Vo so that the body will hit the point A after leaving the track at its highest point. The arrangement is shown in the figure, given that the straight part is rough & the curved path is smooth. The coefficient of friction is μ.
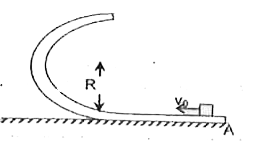
Let the block escape the point at C with a velocity V horizontally. Since it hits the initial spot A after falling through a height 2R we can write
(2R)=12gt2, whrer t= time of its fall.
⇒t=2√R/g
∴ The distance AB=2v√R/g
⇒d=2vx√R/g ...(a)
Work energy theorem is applied to the motion of the body from A to B leads ΔKE=Wf
⇒12mv2o−12mv21=μmgd
⇒vo=√v21+2μgd ...(b)
Energy conservation between B & C yields
12mv21−12mv2=mg(2R)
⇒v1=√v2+4gR ...(c)
When the block escapes C, its minimum speed v can be given as mv2R=mg
( ∴ the normal contact force =0)
⇒v=√gR ...(d)
(Note that if the particle has speed less than √gR then it will not reach to the highest point of the curvature.
By using (c) and (d) we obtain
v1=√5gR ...(e)
using (a) and (d) we obtain
d=(√gR)2(√Rg)=2R ...(f)
vo=√5gR+2μg(2R)=√(5+4μ)gR.

Similar Questions
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
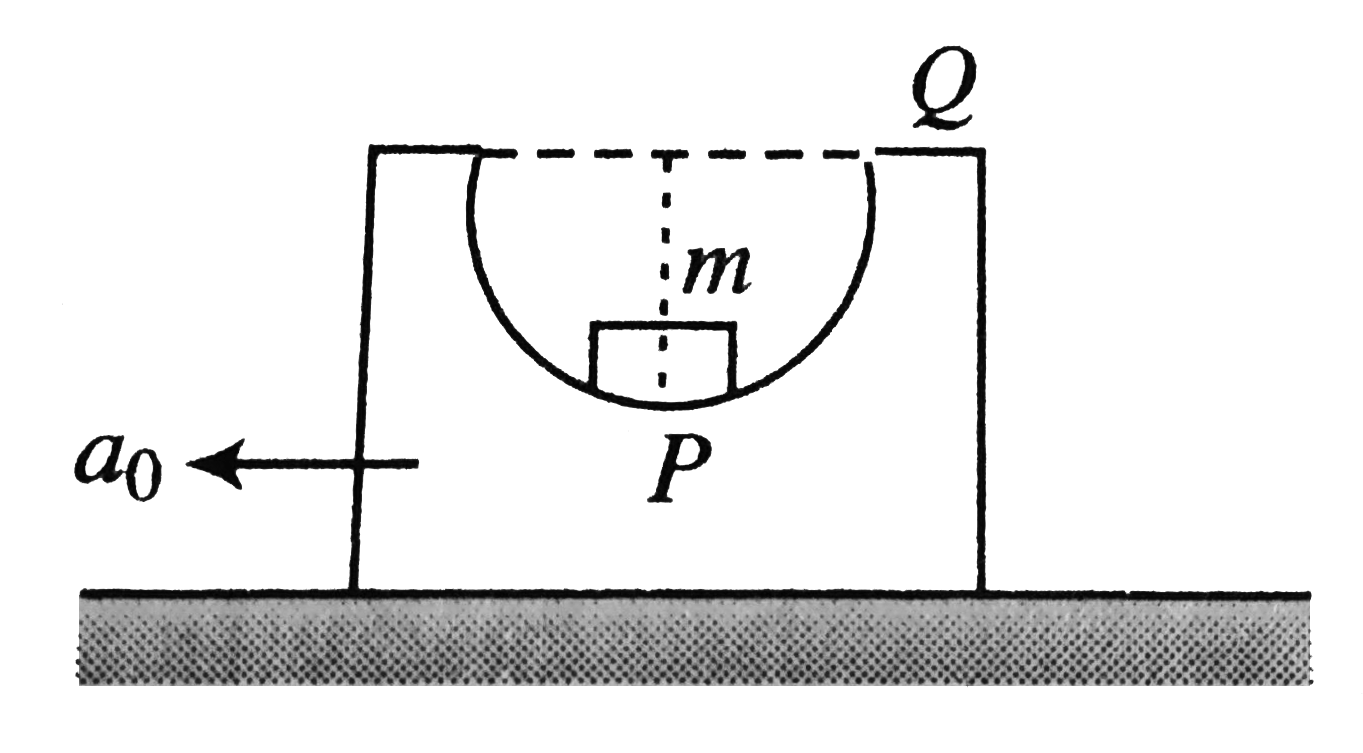
View SolutionA block of mass m is lying at rest at point P of a wedge having a smooth semi-circular track of radius R. What should be the minimum value of a0 so that the mass can just reach point Q
View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
View SolutionA body is projected horizontally with a speed v0 find the velocity of the body when it covers equal distance in horizontal and vertical directions.
View Solution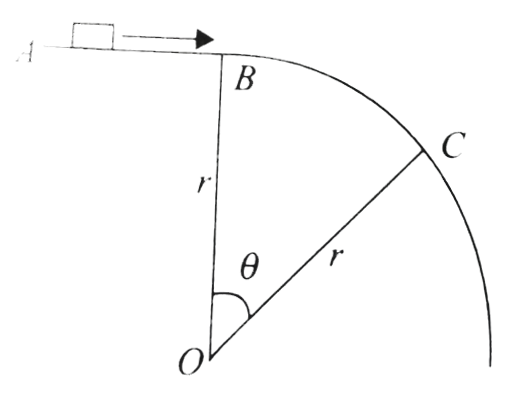
A small block slides with velocity v0=0.5√gr on the horizontal frictiohnless surface as shown in the fig. the block leaves the surface at point C. The angle θ in the figure is:
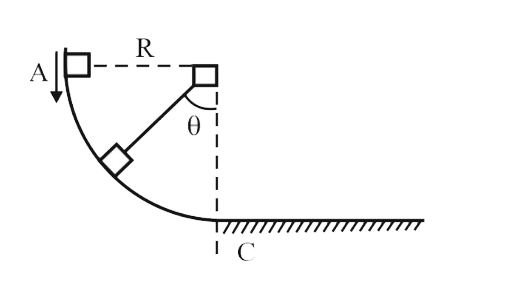
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
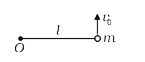
View SolutionA block is released from rest at the top of an inclined plane which later curves into a circular track of radius r as shown in figure. Find the minimum height h from where it should be released so that it is able to complete the circle.
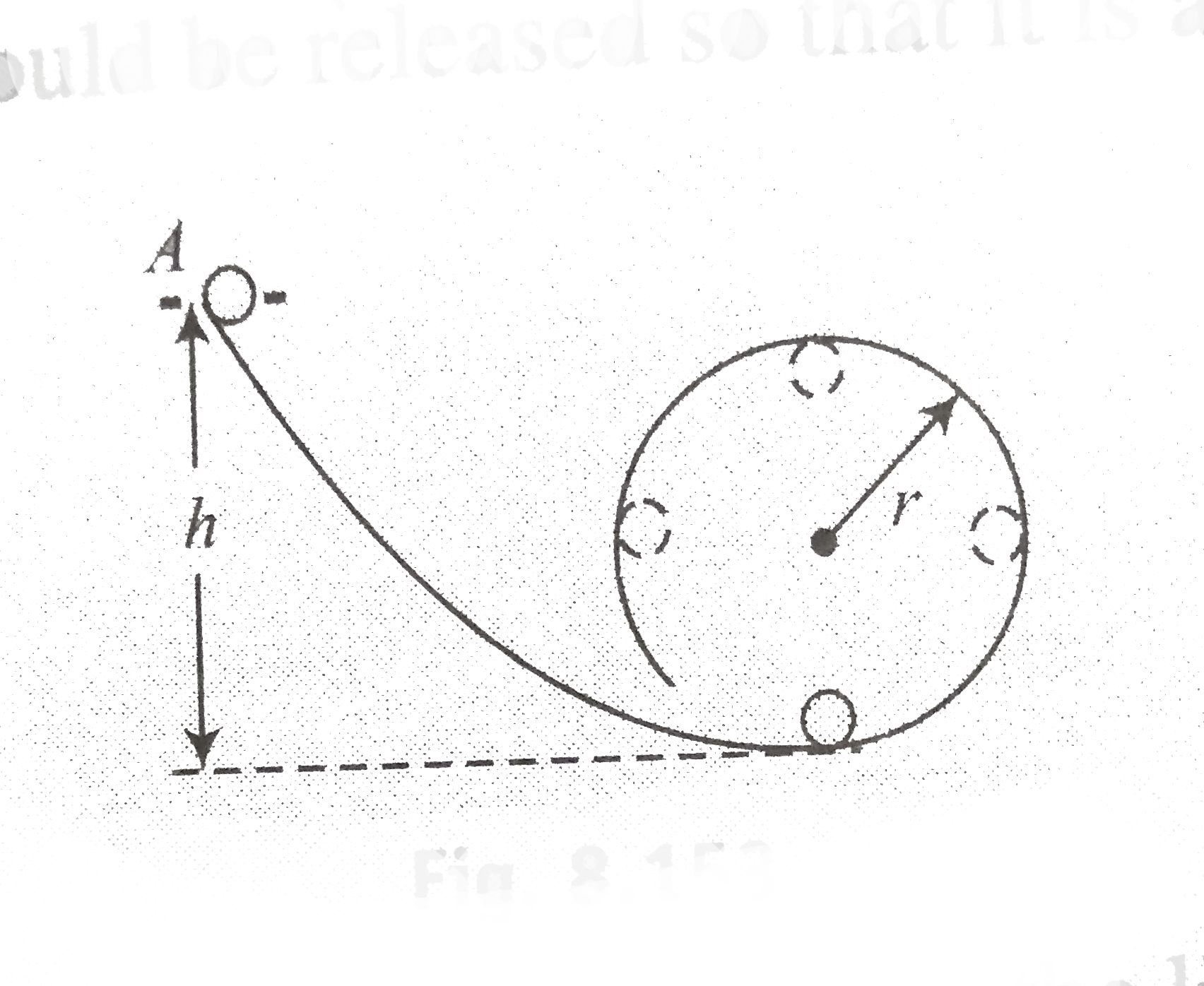
View Solution