The speed of a man in a ponds is double that of the water ina river. The man starts swimming from a polints P on the bank. What is the angle of swimming of the man so as to directly to the opposite bank?
To solve the problem of determining the angle at which a man should swim to reach the opposite bank of a river directly, we can follow these steps:
1. Define Variables:
- Let the speed of the river (water) be v.
- The speed of the man in still water (pond) is given as double that of the river, so it is 2v.
2. Understand the Motion:
- The man swims at an angle θ with respect to the direction perpendicular to the riverbank.
- The goal is for the resultant velocity of the man to be directly across the river (perpendicular to the river flow).
3. Set Up the Velocity Components:
- The velocity of the man relative to the river can be broken down into two components:
- A component perpendicular to the river: Vmrcos(θ)
- A component parallel to the river (in the direction of the river flow): Vmrsin(θ)
Here, Vmr is the man's speed in still water, which is 2v.
4. Write the Equations:
- The component of the man's velocity that counters the river's flow must equal the river's speed for him to reach directly across:
Vmrsin(θ)=v
- The component of the man's velocity that takes him across the river is:
Vmrcos(θ)=2vcos(θ)
5. Relate the Components:
- From the equation Vmrsin(θ)=v, we can substitute Vmr=2v:
2vsin(θ)=v
- Dividing both sides by v (assuming v≠0):
2sin(θ)=1
- Therefore, we find:
sin(θ)=12
6. Find the Angle:
- The angle θ that satisfies sin(θ)=12 is:
θ=30∘
Conclusion
The angle at which the man should swim to reach the opposite bank directly is 30∘ with respect to the line perpendicular to the riverbank.
- Let the speed of the river (water) be v.
- The speed of the man in still water (pond) is given as double that of the river, so it is 2v.
- The man swims at an angle θ with respect to the direction perpendicular to the riverbank.
- The goal is for the resultant velocity of the man to be directly across the river (perpendicular to the river flow).
- The velocity of the man relative to the river can be broken down into two components:
- A component perpendicular to the river: Vmrcos(θ)
- A component parallel to the river (in the direction of the river flow): Vmrsin(θ)
- The component of the man's velocity that counters the river's flow must equal the river's speed for him to reach directly across:
Vmrsin(θ)=v
- The component of the man's velocity that takes him across the river is:
Vmrcos(θ)=2vcos(θ)
- From the equation Vmrsin(θ)=v, we can substitute Vmr=2v:
2vsin(θ)=v
- Dividing both sides by v (assuming v≠0):
2sin(θ)=1
- Therefore, we find:
sin(θ)=12
- The angle θ that satisfies sin(θ)=12 is:
θ=30∘
The angle at which the man should swim to reach the opposite bank directly is 30∘ with respect to the line perpendicular to the riverbank.
Similar Questions
In the figure shown a river of width 4m is flowing with speed of 5m/s. A swimmer whose swimming speed relative to the water is 4ms, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (in m) the swimmer will have to walk on the other bank to reach the point B.
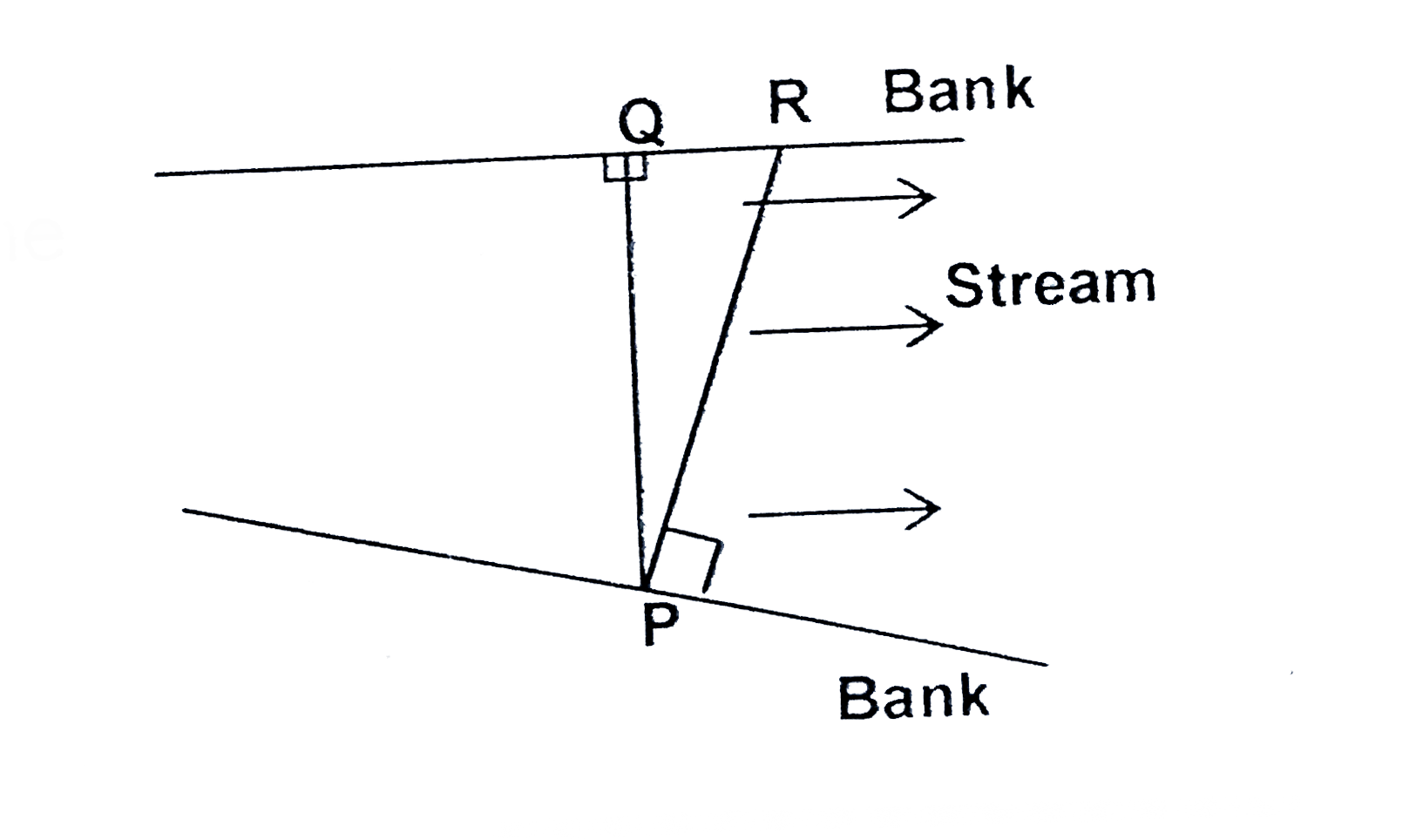
View SolutionIn a lake, stream direction is as shown in the figure. A man starting from the point P on the bank wants to move to the otherside of the bank in shortest time .Then direction in which he should swim
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
View SolutionA person is standing at the edge of a slow moving river which is 1 km wide. He wishes to return to the camp ground on the opposite side of the river for which he may swim to any point on the opposite bank and then walk for the rest of the distance. The campground is 1 km away from the point on the opposite bank directly across from where he starts to swim. If he swims at the rate of 2 km/hr and walks at the rate of 3 km/hr, the minimum time taken by him is approximately 0.6 hr (b) 0.7 hr (c) 0.8 hr (d) 0.9 hr
View SolutionA T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite to the tower, the angle of elevation of the top of the tower is 60 degrees. From a point 20m away this point on the same bank, the angle of elevation of the top of the tower is 30o . Find the height of the tower and the width of the river.
View SolutionA man can swim in still water with a speed of 3m/s x and y axis are drawn along and normal to the bank of river flowing to right with a speed of 1m/s. The man starts swimming from origin O at t = 0 second. Assume size of man to be negligible. Find the equation of locus of all the possible points where man can reach at t = 1 sec

View SolutionA swimmer can swim in still water with speed v and the river is flowing with speed v/2. What is the ratio of the time taken to swimming across the river in shortest time to that of swimming across the river over the shortest distance ?
View SolutionIn a river of 20 m width. Half part of river flows with speed 10m/sec and remaining half part flows with 20m/sec as shown in figure. A man starts to swim from A and reaches to point B in 10 sec. Man swims with speed Vm with respect to river at an angle θ with line AB. Then, angle θ will be : (man swims with constant speed and in same direction with respect to river throughout the motion):
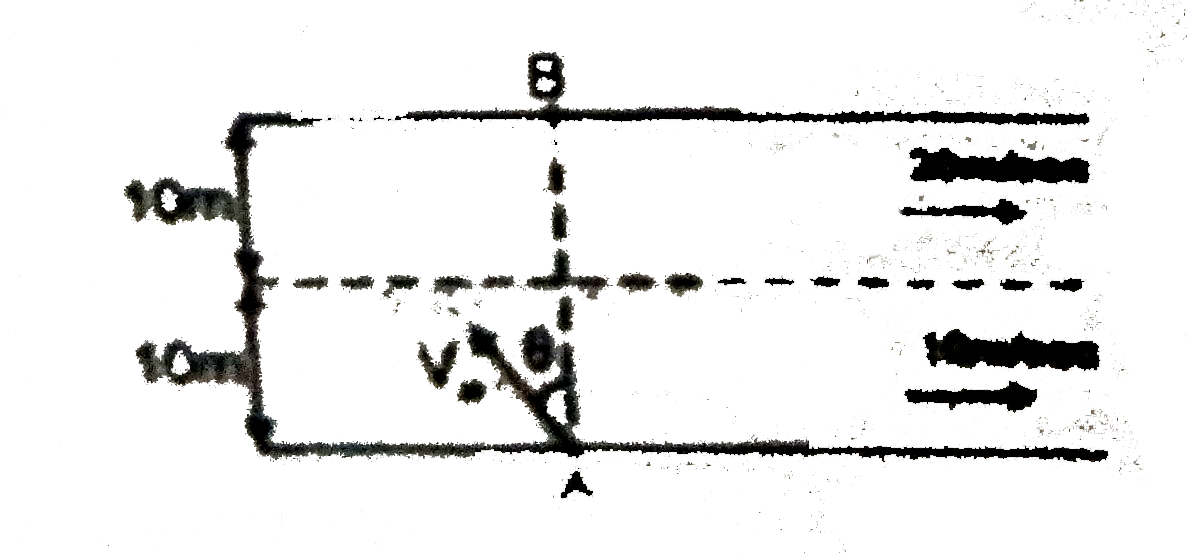
View SolutionA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .
.
View SolutionA man can swim at a speed 2ms−1 in still water. He starts swimming in a river at an angle 150∘ with direction of flow of water and reaches at the exactly oppsite point on the opposite bank.
(a) Find the speed of flowing water.
(b) If width of river is 1 km then calculate the time taken also
View Solution
