A body is dropped from a height h=50 m. Another body is projected vertically up with a speed V=10 m//sec after a time t0= 2 sec from the instant of release of the first body. Find the time of their meetings.
To solve the problem, we need to analyze the motion of both bodies separately and then find the time at which they meet.
Step 1: Define the motion of the first body
The first body is dropped from a height of h=50m. Since it is dropped, its initial velocity u1=0. The distance fallen by the first body after time t is given by the equation of motion:
S1=u1t+12gt2
Substituting u1=0:
S1=12gt2
Where g≈9.8m/s2.
Step 2: Define the motion of the second body
The second body is projected upwards with an initial velocity V=10m/s after a delay of t0=2s. Therefore, the time of flight for the second body when they meet is t−2. The distance traveled by the second body is given by:
S2=V(t−2)−12g(t−2)2
Substituting V=10m/s:
S2=10(t−2)−12g(t−2)2
Step 3: Set up the equation for meeting point
The two bodies meet when the sum of the distances they have traveled equals the initial height from which the first body was dropped:
S1+S2=h
Substituting the equations for S1 and S2:
12gt2+(10(t−2)−12g(t−2)2)=50
Step 4: Substitute g and simplify
Using g=10m/s2 for simplicity:
12⋅10t2+(10(t−2)−12⋅10(t−2)2)=50
This simplifies to:
5t2+(10t−20−5(t2−4t+4))=50
Expanding and simplifying:
5t2+10t−20−5t2+20t−20=50
Combining like terms:
30t−40=50
Step 5: Solve for t
Adding 40 to both sides:
30t=90
Dividing by 30:
t=3s
Conclusion
The time at which the two bodies meet is t=3s.
---
The first body is dropped from a height of h=50m. Since it is dropped, its initial velocity u1=0. The distance fallen by the first body after time t is given by the equation of motion:
S1=u1t+12gt2
Substituting u1=0:
S1=12gt2
Where g≈9.8m/s2.
The second body is projected upwards with an initial velocity V=10m/s after a delay of t0=2s. Therefore, the time of flight for the second body when they meet is t−2. The distance traveled by the second body is given by:
S2=V(t−2)−12g(t−2)2
Substituting V=10m/s:
S2=10(t−2)−12g(t−2)2
The two bodies meet when the sum of the distances they have traveled equals the initial height from which the first body was dropped:
S1+S2=h
Substituting the equations for S1 and S2:
12gt2+(10(t−2)−12g(t−2)2)=50
Using g=10m/s2 for simplicity:
12⋅10t2+(10(t−2)−12⋅10(t−2)2)=50
This simplifies to:
5t2+(10t−20−5(t2−4t+4))=50
Expanding and simplifying:
5t2+10t−20−5t2+20t−20=50
Combining like terms:
30t−40=50
Adding 40 to both sides:
30t=90
Dividing by 30:
t=3s
The time at which the two bodies meet is t=3s.
Similar Questions
A body is thrown vertically up with a velocity of 100 m/s and another one is thrown 4 sec after the first one. How long after the first one is thrown will they meet?
View SolutionAssertion : A body is dropped from height h and another body is thrown vertically upwards with a speed √gh. They meet at height h2.
Reason : The time taken by both the blocks in reaching the height h2 is same.
View SolutionA stone is dropped from a height 300 m and at the same time another stone is projected vertically upwards with a velocity of 100m/sec. Find when and where the two stones meet.
View SolutionA body is projected horizontally with speed 30m/s from a very high tower. What will be its speed after 4sec-
View SolutionA body is projected vertically upwards with a speed of √GMR ( M is mass and R is radius of earth ) . The body will attain a height of
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
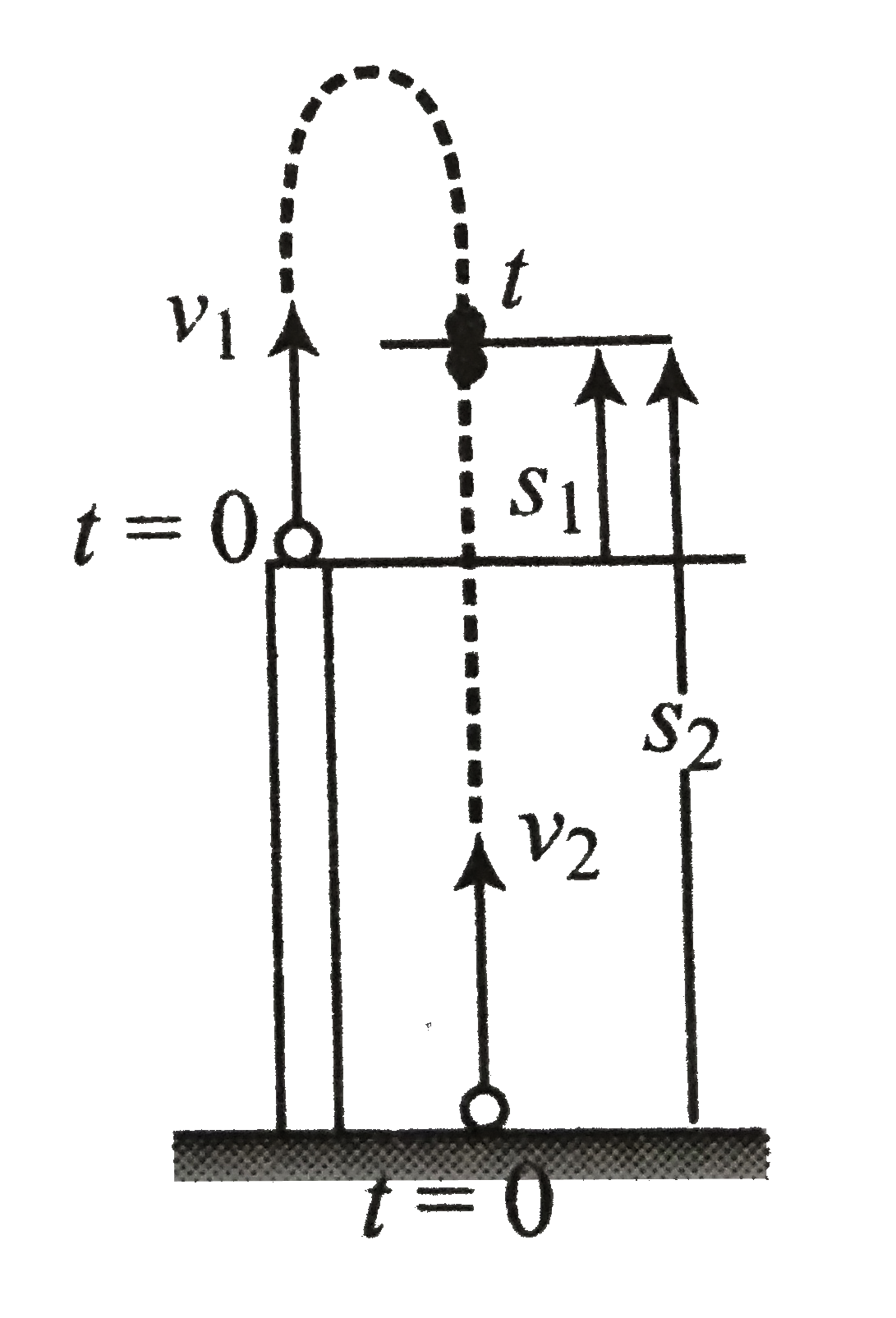
View SolutionA body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
View SolutionA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
View SolutionA stone is dropped from a tower of height 200 m and at the same time another stone is projected vertically up at 50 m/s. The height at which they meet ? [g=10m/s2]
View SolutionBall A is thrown up vertically with speed 10ms. At the same instant another ball B is released from rest at height h. At time t, the speed of A relative to B is
View Solution

