Question

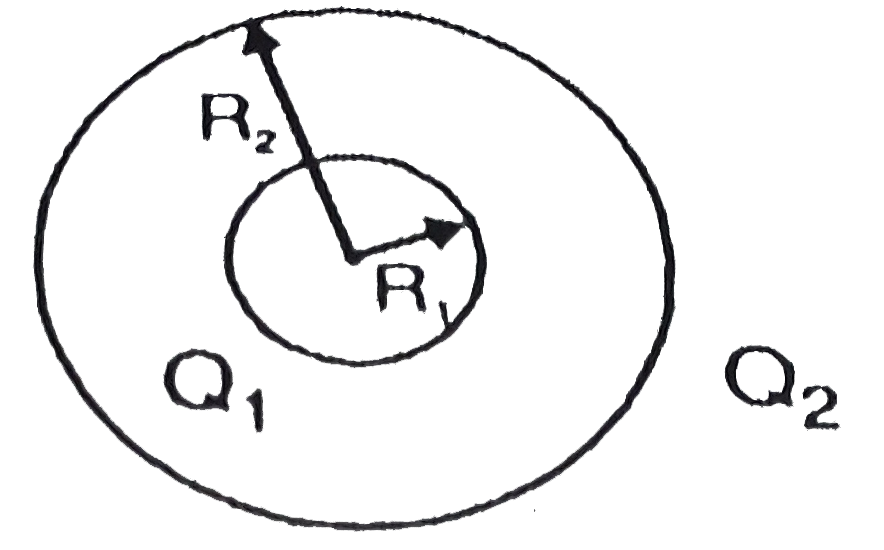
The space between the two coaxial cylindrical shells of radius $R_1\text{and}{R}_2(R_1<R_2)$ is filled by a dielectric substance, whose dielectric constant varies with the distance from the axis as $k=A/r^3$. If the length of the cylindrical shells is $l$ then find the capacitance of the system

Explanation

To find the capacitance of the coaxial cylindrical shells filled with a dielectric whose dielectric constant varies with distance, we follow these steps:

Step 1: Understand the Geometry and Variables
We have two coaxial cylindrical shells with inner radius \( R_1 \) and outer radius \( R_2 \). The dielectric constant \( k \) varies with distance \( r \) from the axis as \( k = \frac{A}{r^3} \), where \( A \) is a constant.

Step 2: Electric Field Calculation
The electric field \( E \) between the two cylindrical shells can be derived from Gauss's law. The electric field in the region between the cylinders is given by:
\( E = \frac{Q}{2 \pi \epsilon_0 k r} \)
Substituting the expression for \( k \):
\( E = \frac{Q}{2 \pi \epsilon_0 \left(\frac{A}{r^3}\right) r} = \frac{Q r^2}{2 \pi \epsilon_0 A} \)

Step 3: Calculate the Potential Difference \( V \)
The potential difference \( V \) between the two shells is obtained by integrating the electric field from \( R_1 \) to \( R_2 \):
\( V = -\int_{R_1}^{R_2} E \, dr \)
Substituting the expression for \( E \):
\( V = -\int_{R_1}^{R_2} \frac{Q r^2}{2 \pi \epsilon_0 A} \, dr \)

Step 4: Evaluate the Integral
Calculating the integral:
\( V = -\frac{Q}{2 \pi \epsilon_0 A} \int_{R_1}^{R_2} r^2 \, dr \)
The integral of \( r^2 \) is:
\( \int r^2 \, dr = \frac{r^3}{3} \)
Thus,
\( V = -\frac{Q}{2 \pi \epsilon_0 A} \left( \frac{R_2^3}{3} - \frac{R_1^3}{3} \right) = -\frac{Q}{6 \pi \epsilon_0 A} (R_2^3 - R_1^3) \)

Step 5: Calculate Capacitance \( C \)
The capacitance \( C \) is defined as:
\( C = \frac{Q}{V} \)
Substituting the expression for \( V \):
\( C = \frac{Q}{-\frac{Q}{6 \pi \epsilon_0 A} (R_2^3 - R_1^3)} = -6 \pi \epsilon_0 A \frac{1}{(R_2^3 - R_1^3)} \)

Final Result
Thus, the capacitance of the system is:
\( C = \frac{6 \pi \epsilon_0 A}{R_2^3 - R_1^3} \)