A man on the top of a cliff 100 meter high, observes the angles of depression of two points on the opposite sides of the cliff as 30∘ and 60∘ respectively. Find the difference between the two points.
The correct Answer is:=400√3 meters.
To solve the problem step by step, we will use trigonometric relationships based on the angles of depression observed from the top of the cliff.
1. Understanding the Problem:
- A man is standing at the top of a cliff that is 100 meters high.
- He observes two points (A and B) on opposite sides of the cliff with angles of depression of 30° and 60°, respectively.
2. Drawing the Diagram:
- Draw a vertical line representing the cliff (height = 100 m).
- Mark the top of the cliff as point C (where the man is).
- Mark the two points on the ground as A and B.
- Draw horizontal lines from C to points A and B, forming two right triangles: triangle ACO and triangle BCO.
3. Identifying Angles and Sides:
- The angle of depression to point A is 30°.
- The angle of depression to point B is 60°.
- The height of the cliff (CO) is 100 m.
4. Using Trigonometry for Point B:
- In triangle BCO, we can use the tangent function:
tan(60°)=BOCO
- Here, BO is the horizontal distance from point B to the base of the cliff (point O).
- Substituting the known values:
tan(60°)=√3andCO=100 m
√3=BO100
- Rearranging gives:
BO=100⋅√3 m
5. Using Trigonometry for Point A:
- In triangle ACO, we again use the tangent function:
tan(30°)=AOCO
- Here, AO is the horizontal distance from point A to the base of the cliff (point O).
- Substituting the known values:
tan(30°)=1√3andCO=100 m
1√3=AO100
- Rearranging gives:
AO=100⋅1√3=100√3 m
6. Finding the Difference Between Points A and B:
- The total distance between points A and B (AB) is:
AB=AO+BO
- Substituting the values we found:
AB=100√3+100√3
- To add these fractions, we need a common denominator:
AB=100√3+100⋅3√3=100+300√3=400√3 m
7. Final Answer:
- The difference between the two points A and B is:
AB=400√3 m
- A man is standing at the top of a cliff that is 100 meters high.
- He observes two points (A and B) on opposite sides of the cliff with angles of depression of 30° and 60°, respectively.
- Draw a vertical line representing the cliff (height = 100 m).
- Mark the top of the cliff as point C (where the man is).
- Mark the two points on the ground as A and B.
- Draw horizontal lines from C to points A and B, forming two right triangles: triangle ACO and triangle BCO.
- The angle of depression to point A is 30°.
- The angle of depression to point B is 60°.
- The height of the cliff (CO) is 100 m.
- In triangle BCO, we can use the tangent function:
tan(60°)=BOCO
- Here, BO is the horizontal distance from point B to the base of the cliff (point O).
- Substituting the known values:
tan(60°)=√3andCO=100 m
√3=BO100
- Rearranging gives:
BO=100⋅√3 m
- In triangle ACO, we again use the tangent function:
tan(30°)=AOCO
- Here, AO is the horizontal distance from point A to the base of the cliff (point O).
- Substituting the known values:
tan(30°)=1√3andCO=100 m
1√3=AO100
- Rearranging gives:
AO=100⋅1√3=100√3 m
- The total distance between points A and B (AB) is:
AB=AO+BO
- Substituting the values we found:
AB=100√3+100√3
- To add these fractions, we need a common denominator:
AB=100√3+100⋅3√3=100+300√3=400√3 m
- The difference between the two points A and B is:
AB=400√3 m
Similar Questions
There are two points on the horizontal line passing through the foot of a tower in the same side of the tower. The angle of depression of these point from the top of the tower are 45∘ and 60∘ respectively. Find the distance between the two point if the height if the tower is 150 metres.
View SolutionAn observer on the top of a cliff, 200 m above the sea-level, observes the angles of depression of the two ships to be 45∘and30∘ respectively. Find the distance between the ships, if the ships are
on the opposite sides of the cliff
View SolutionAn observer on the top of a cliff, 200 m above the sea-level, observes the angles of depression of the two ships to be 45∘and30∘ respectively. Find the distance between the ships, if the ships are
on the same side of the cliff,
View SolutionTwo men on either side of the cliff 80m high observes the angles of elevation of the top of the cliff to be 30o and 60o respectively. Find the distance between the two men.
View SolutionAs observed from the top of a 80 m tall lighthouse, the angle of depression of two ships, on the same side of the light house in horizontal line with its base, are 30∘and40∘ respectively . Find the distance between the two ships. Given your answer correct to the nearest metre
View SolutionAn aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45∘and60∘ respectively. Find the width of the river. Write the answer correct to the nearest whole number.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the difference between the heights of the building and the lamp post.
View SolutionFrom the top of a light house 100 m high, t he angles of depression of two ships are observed as 48∘and36∘ respectively. Find the distance between the two ships (in the nearest metre ) if :
the ships are on the same side of the light house.
View SolutionIf from the top of a tower, 60 meters high, the angles of depression of the top an floor of a house are 30∘and60∘ respectively, then the height (in meters) of the house is
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
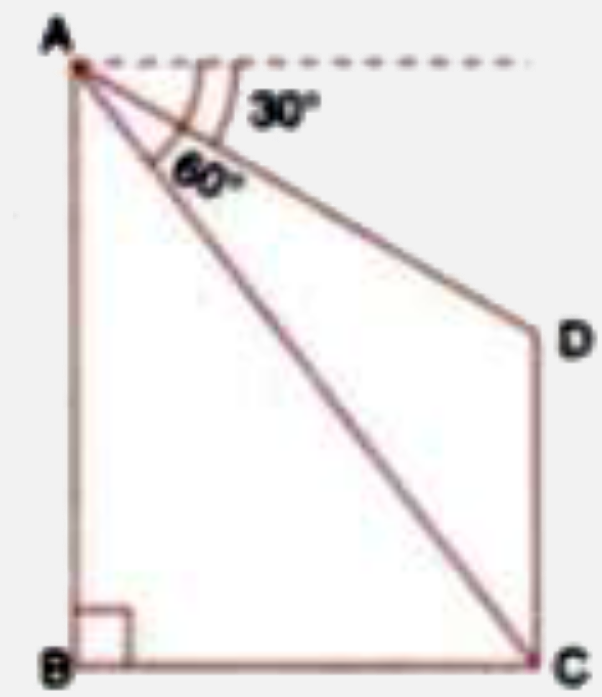
the horizontal distance between AB and CD
View Solution

