A uniform rod AB of mass M and length √2R is moving in a veritcal plane inside a hollow sphere of radius R. The sphere is rolling on a fixed horizontal surface without slipping with velocity of its centre of mass 2v. When the end B is the lowest position, its speed is found to be v as shown in the figure. If the kinetic energy of the rod at this instant is 4KMv2. Find K.
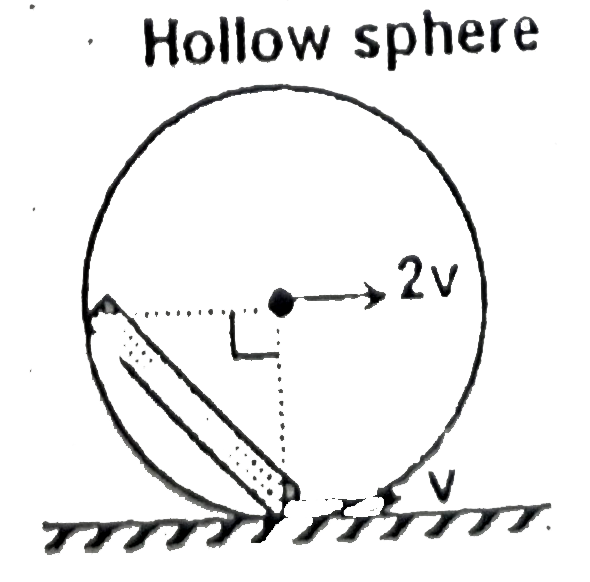
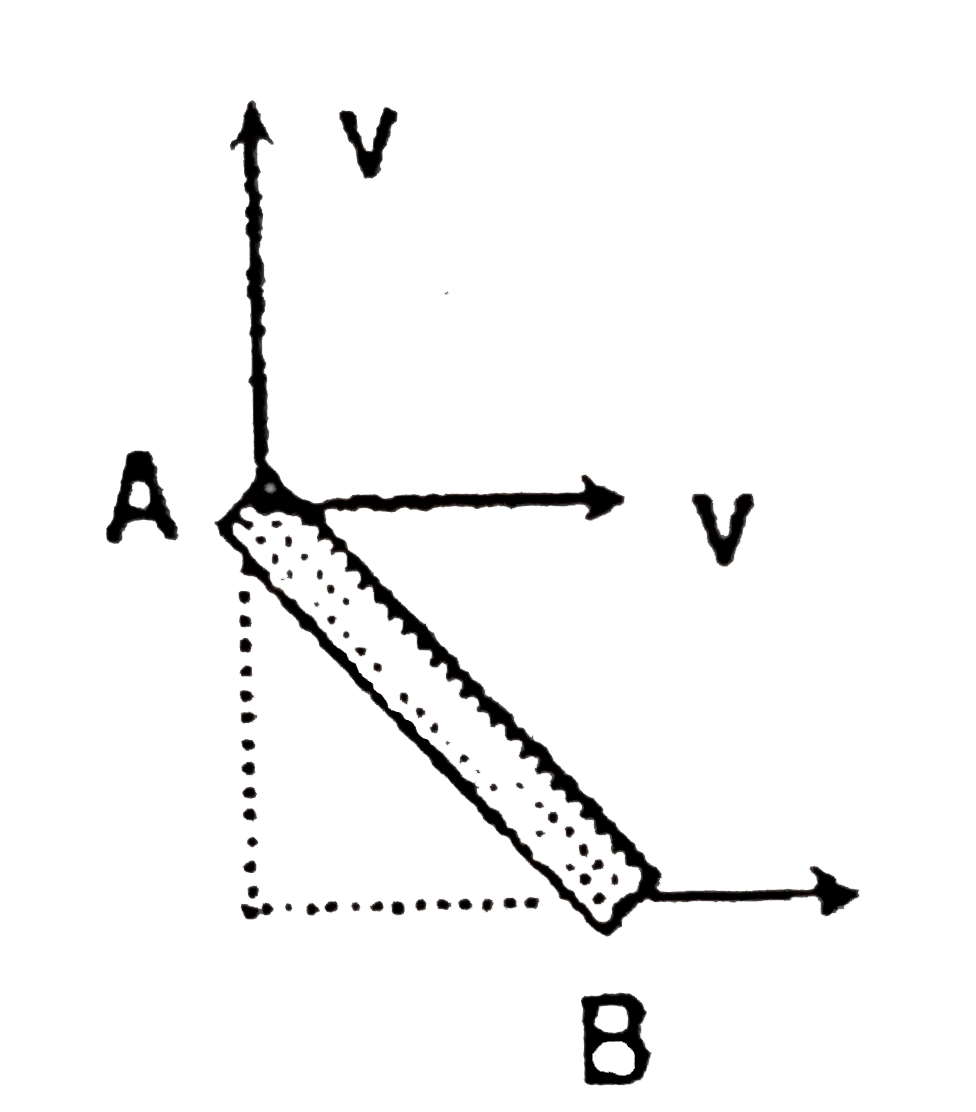
Let the velocity of the point A have components 2V along horizontal, v1 along the vertical.
Since the rod AB is rigid, taking the velocities along the rod AB,
2vcos45∘−v1cos45∘=vcos45∘
or v1=v
The angular velocity of the rod AB equals (in the frame in which end B is at rest)
ω=√2v√2R=vR
The velocity of the C.M. of AB
Where ˆi,ˆj are the unit vectors along the horizontal and vertical (upward) direction respectively.
The K.E. of the rod AB
=12Mv2CM+12ICMω2=12M(9v24+v24)+12112M(√∘R)2(vR)2=43Mv2
Similar Questions
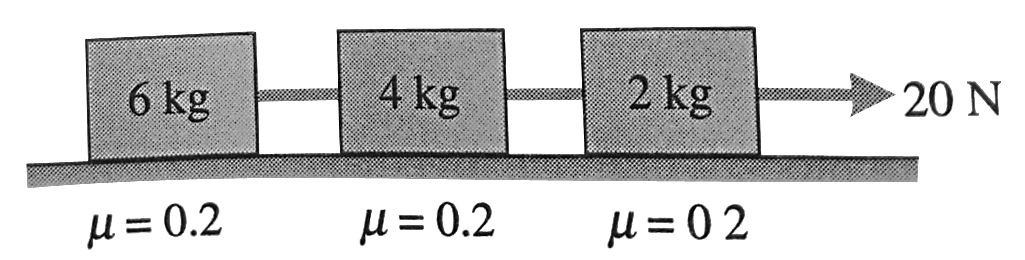
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
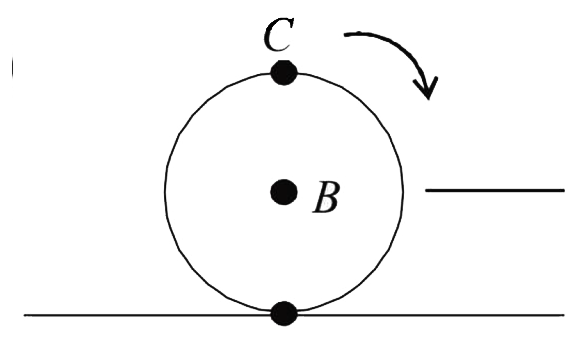
A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View Solution
