A particle moves towards a concave mirror of focal length along its axis and with a constant speed of . At the instant the particle is from the pole
velocity of image is
velocity of image w.r.t. particle is
particle and image move towards each other
as the particle approaches pole, velocity of image increases
To solve the problem step by step, we will use the mirror formula and the concept of image velocity in relation to object velocity.
Step 1: Identify the given values
- Focal length of the concave mirror, f=−30cm (negative for concave mirrors)
- Object distance, u=−90cm (negative as per sign convention)
- Speed of the object, dudt=−4cm/s (negative because the object is moving towards the mirror)
Step 2: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
Rearranging this to find v:
1v=1f−1u
Step 3: Substitute the values into the mirror formula
Substituting the values of f and u:
1v=1−30−1−90
Calculating the right-hand side:
1v=−130+190
Finding a common denominator (which is 90):
1v=−390+190=−290=−145
Thus, we find:
v=−45cm
Step 4: Calculate the velocity of the image
Using the relationship between the velocities of the object and image:
dvdt=−v2u2⋅dudt
Substituting the known values:
dvdt=−(−45)2(−90)2⋅(−4)
Calculating (−45)2(−90)2:
dvdt=−20258100⋅(−4)=−14⋅(−4)=1cm/s
Step 5: Find the relative velocity of the image with respect to the object
The relative velocity of the image with respect to the object is given by:
Velocity of image w.r.t object=dvdt−dudt
Substituting the values:
Velocity of image w.r.t object=1−(−4)=1+4=5cm/s
Final Answer
The velocity of the image with respect to the object is 5cm/s towards the mirror.
---
- Focal length of the concave mirror, f=−30cm (negative for concave mirrors)
- Object distance, u=−90cm (negative as per sign convention)
- Speed of the object, dudt=−4cm/s (negative because the object is moving towards the mirror)
The mirror formula is given by:
1f=1v+1u
Rearranging this to find v:
1v=1f−1u
Substituting the values of f and u:
1v=1−30−1−90
Calculating the right-hand side:
1v=−130+190
Finding a common denominator (which is 90):
1v=−390+190=−290=−145
Thus, we find:
v=−45cm
Using the relationship between the velocities of the object and image:
dvdt=−v2u2⋅dudt
Substituting the known values:
dvdt=−(−45)2(−90)2⋅(−4)
Calculating (−45)2(−90)2:
dvdt=−20258100⋅(−4)=−14⋅(−4)=1cm/s
The relative velocity of the image with respect to the object is given by:
Velocity of image w.r.t object=dvdt−dudt
Substituting the values:
Velocity of image w.r.t object=1−(−4)=1+4=5cm/s
The velocity of the image with respect to the object is 5cm/s towards the mirror.
Similar Questions
For a concave mirror of focal length 20 cm, match the following

View SolutionFrom a concave mirror of focal length 20 cm. match the following:

View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionAn object is moving towards a concave mirror of focal length 24 cm. When it is at a distance of 60 cm from the mirror, its speed is 9cm/s. The speed of its image at that instant , is
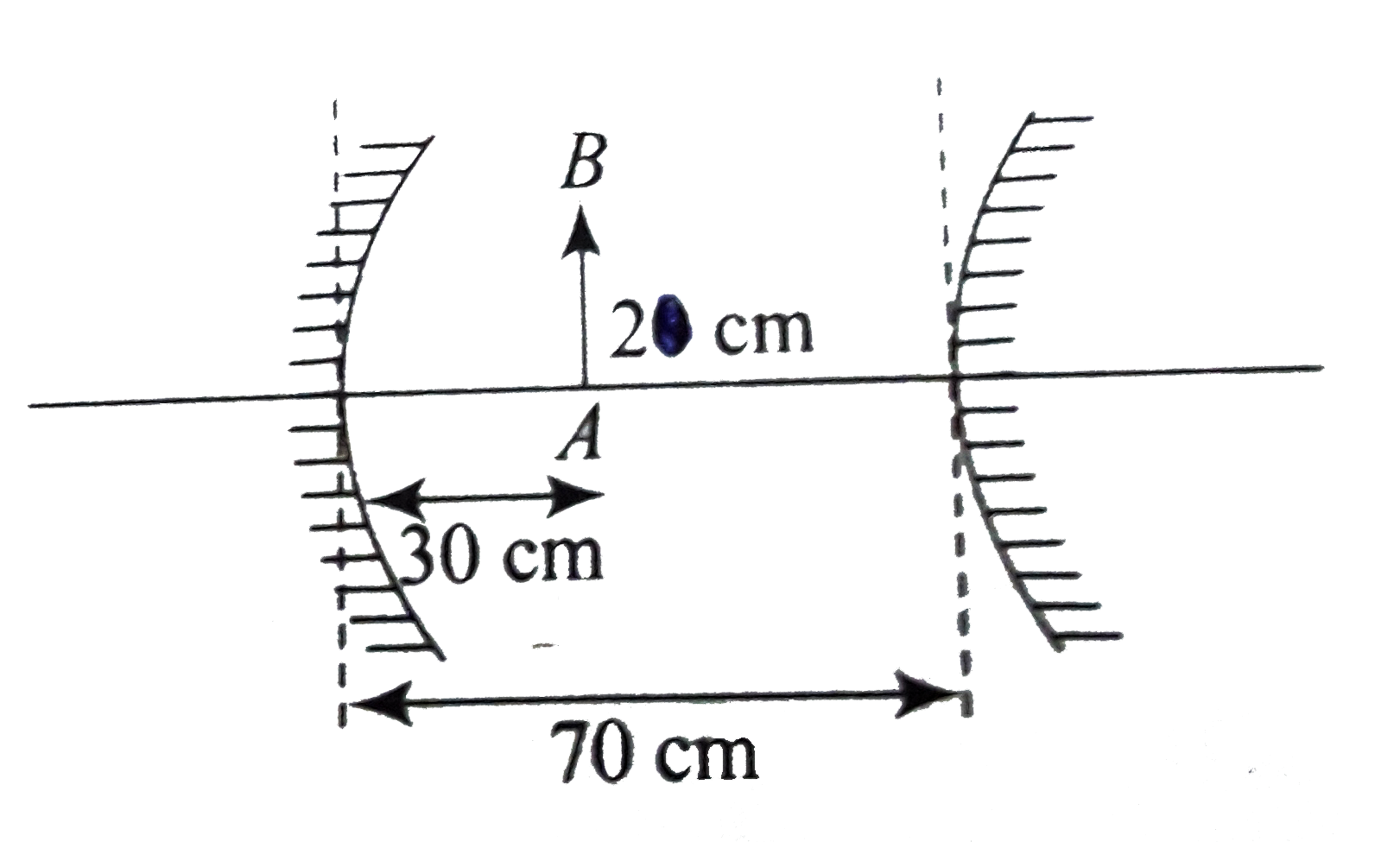
View SolutionA concave mirror and a convex mirror of focal lengths 10cm and 15cm are places at a distance of 70cm. An object AB of height 2cm is places at a distance of 30cm from the concave mirror. First ray is incident on the concave mirror then on the convex mirror. Find size, position, and nature of the image.
View SolutionAn object is at 20 cm from a concave mirror of focal length 10 cm, the nature of image is
View SolutionDetermine the position of the image produced by an optical system consisting of a concave mirror with a focal length of 10cm and a convergent lens with a focal length of 20cm. The distance from the mirror to the lens is 30cm and from the lens to the object is 40cm. Consider only two steps. Plot the image.
View SolutionA particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that the end closer to the pole is 20 cm away from it. Find the length of the image.
View SolutionA rod of length 10 cm lies along the principal axis of a concave mirror of focal length 10 cm in such a way that its end closer to the pole is 20cm away from the mirror. The length of the image is
View Solution